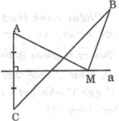
Cho hình bên, M là một điểm tùy ý nằm trên đường thẳng a. Vẽ điểm C sao cho a là đường trung trực của AC. Tìm vị trí của điểm M trên đường thẳng a để MA + MB là nhỏ nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2022
a: Gọi N là giao điểm của BC với a
Nếu M khác N
Vì M nằm trên đường trung trực của AC
nên MA=MC
XétΔMBC có BC<MB+MC
=>BC<MA+MB
Nếu M trùng với N thì nối NA
Vì N nằm trên đường trung trực của AC nên NA=NC
=>MA+MB=NA+NB=BC
=>MA+MB>=BC
b: MA+MB nhỏ nhất khi M là giao điểm của BC với a
CM
25 tháng 3 2018
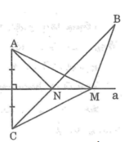
Gọi N là giao điểm của BC với đường thẳng a.
* Nếu M ≠ N
Nối MC.
Vì a là đường trung trực của AC và M ∈ a
Suy ra: MA = MC (tính chất đường trung trực) (1)
Trong ΔMBC, ta có:
BC < MB + MC (bất đẳng thức tam giác) (2)
Thay (1) vào (2) ta có: BC < MA + MB
* Nếu M trùng với N
Nối NA. Ta có:
NA = NC (tính chất đường trung trực)
Mà: MA + MB = NA + NB = NC + NB = BC
Vậy: MA + MB ≥ BC
LN
4 tháng 5 2018
a)Nối M với C. Vì a là trung trực của AC mà M thuộc a nên
MA=MC
Mà tam giác MBC có:
MB+MC>BC (Bđt tam giác)
Suy ra: MB+MA>BC
Vậy MA+MB>BC
b) Mik không biết trình bày làm sau nhưng M là trung điểm của AC thì MA+MB nhỏ nhất
Theo chứng minh trên, khi M trùng với N thì MA + MB = BC bé nhất. Vậy khi M là giao điểm của BC với đường thẳng a thì MA + MB bé nhất.