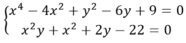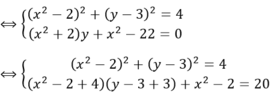giải phương trinh : x2 +y2 +6y + 5 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.

Ta xét các phương án:
(I) có:
![]()
(II) có:
![]()
(III) tương đương : x2+ y2 – 2x - 3y + 0,5= 0.
phương trình này có:
![]()
Vậy chỉ (I) và (III) là phương trình đường tròn.
Chọn D.

Đường tròn (C): x 2 + y 2 + 8 x + 6 y + 5 = 0 có tâm I( - 4; -3) và bán kính R = 20
Khoảng cách I , ∆ = 3. − 4 − 4. − 3 − 10 5 = 2 < R nên đường thẳng cắt đường tròn tại hai điểm A, B cách nhau một khoảng là A B = 2 √ ( R 2 - ( d ( I , ∆ ) ) 2 ) = 8
ĐÁP ÁN D

Đường tròn (C) có tâm I( -1;3) và bán kính. R = 1 + 9 - 5 = 5
Do tiếp tuyến d song song với đường thẳng a nên d có dạng: x + 2y - m = 0
d là tiếp tuyến của (C) khi và chỉ khi:
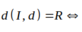
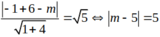
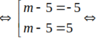
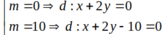
Chọn A.

Đáp án D
Trong các dây của đường tròn; dây lớn nhất là đường kính. Nên để d cắt (C) theo 1 dây cung dài nhất thì d phải đi qua tâm I ( -2; 3) của đường tròn.
Vậy d qua I và A(3;2) nên có VTCP ![]() và có VTPT
và có VTPT ![]()
=> phương trình d: 1( x- 3) + 5( y- 2) = 0 hay x+ 5y – 13= 0
Do đó d: x+ 5y -13= 0 .

Đáp án: A
(C): x 2 + y 2 + 4x - 6y - 3 = 0 ⇔ (x + 2 ) 2 + (y - 3 ) 2 = 16
Đường tròn (C) có tâm I(-2;3) 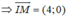
Gọi d là phương trình tiếp tuyến của (C) tại M. Suy ra, d đi qua M và nhận IM là vecto pháp tuyến
⇒ d: 4(x - 2) + 0.(y - 3) = 0 ⇔ x - 2 = 0

Lời giải:
a.
$x^2-x=y^2-1$
$\Leftrightarrow x^2-x+1=y^2$
$\Leftrightarrow 4x^2-4x+4=4y^2$
$\Leftrightarrow (2x-1)^2+3=(2y)^2$
$\Leftrightarrow 3=(2y)^2-(2x-1)^2=(2y-2x+1)(2y+2x-1)$
Đến đây xét các TH:
TH1: $2y-2x+1=1; 2y+2x-1=3$
TH2: $2y-2x+1=-1; 2y+2x-1=-3$
TH3: $2y-2x+1=3; 2y+2x-1=1$
TH4: $2y-2x+1=-3; 2y+2x-1=-1$
b.
$x^2+12x=y^2$
$\Leftrightarrow (x+6)^2=y^2+36$
$\Leftrightarrow 36=(x+6)^2-y^2=(x+6-y)(x+6+y)$
Đến đây xét trường hợp tương tự phần a.
c.
$x^2+xy-2y-x-5=0$
$\Leftrightarrow x^2+xy=x+2y+5$
$\Leftrightarrow 4x^2+4xy=4x+8y+20$
$\Leftrightarrow (2x+y)^2=4x+8y+20+y^2$
$\Leftrightarrow (2x+y)^2-2(2x+y)+1=y^2+6y+21$
$\Leftrightarrow (2x+y-1)^2=(y+3)^2+12$
$\Leftrightarrow (2x+y-1)^2-(y+3)^2=12$
$\Leftrightarrow (2x+y-1-y-3)(2x+y-1+y+3)=12$
$\Leftrightarrow (2x-4)(2x+2y+2)=12$
$\Leftrightarrow (x-2)(x+y+1)=3$
Đến đây đơn giản rồi.
a) \(x^2-x=y^2-1\)
\(\Rightarrow x^2-x+1=y^2\)
\(\Rightarrow4x^2-4x+4=4y^2\)
\(\Rightarrow4x^2-4x+1+3=\left(2y\right)^2\)
\(\Rightarrow\left(2x+1\right)^2-\left(2y\right)^2=-3\)
\(\Rightarrow\left(2x-2y+1\right)\left(2x+2y+1\right)=-3\)
Vì \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}\left(2x-2y+1\right)\left(2x+2y+1\right)\in Z\\\left(2x-2y+1\right)\left(2x+2y+1\right)\inƯ\left(7\right)\end{matrix}\right.\)
Ta có bảng:
| x-y | -1 | 0 | -2 | 1 |
| x+y | 1 | -2 | 0 | -1 |
| x | 0 | -1 | -1 | 0 |
| y | 1 | -1 | -1 | -1 |
Vậy \(\left(x,y\right)\in\left\{\left(0;1\right);\left(-1;-1\right);\left(-1;-1\right);\left(0;-1\right)\right\}\)

Đường tròn (C): x 2 + y 2 + 4 x − 6 y − 3 = 0 có tâm I(-2; 3) và bán kính R = 4.
Khoảng cách d I , ∆ = 3. − 2 − 4.3 − 2 5 = 4 nên đường thẳng tiếp xúc đường tròn.
ĐÁP ÁN B