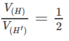Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho BE = EB′/2, DF = FD′/2. Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A’B’C’D’ thành hai khối đa diện (H) và (H’). Gọi (H’) là khối đa diện chứa đỉnh A’. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H’).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 4 2019
Đáp án D
Phương pháp: Sử dụng phương pháp tọa độ hóa.
Cách giải:
Gắn hệ trục Oxyz, có các tia Ox, Oy, Oz lần lượt trùng với các tia AB, AD, AA’.
A(0;0;0), B(1;0;0), C(1;2;0), D(0;2;0), A’(0;0;3), B’(1;0;3), C’(1;2;3), D’(0;2;3)
(P) cắt các tia AB, AD, AA’ lần lượt tại E, F, G (khác A). Gọi E(a;0;0), F(0;b;0), G(0;0;c), (a,b,c > 0)
Phương trình mặt phẳng (P): x a + y b + c z = 1
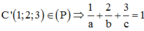
Thể tích tứ diện AEFG: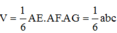 
Ta có: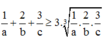 
=>Vmin = 27 khi và chỉ khi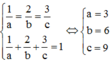 
Khi đó, T = AE + AF + AG = a + b + c = 3 + 6 + 9 = 18
CM
7 tháng 8 2018
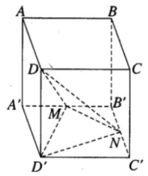
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có: S D ' MN = S A ' B ' C ' D ' - S D ' A ' M + S D ' C ' N + S B ' MN
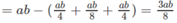
Thể tích khối chóp
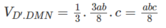
Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng 1/8
CM
17 tháng 8 2019
Đáp án A.
Ta chứng minh được công thức tỷ số thể tích tối với khối hộp như sau (học sinh có thể tự chứng minh).
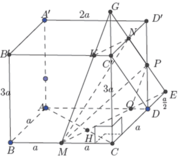
V A ' B ' C ' D ' . M N P Q V A ' B ' C ' D ' . A B C D = 1 2 A ' M A ' A + C ' P C ' C = 1 2 B ' Q B ' B + D N D ' D = 7 2
Do đó thể tích khối đa diện nhỏ hơn là 15 2 V = 5 2 .2018 = 5045 6 .
CM
23 tháng 2 2018
Đáp án D
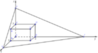
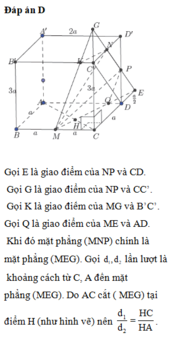
Gọi E là giao điểm của NP và CD. Gọi G là giao điểm của NP và CC’. Gọi K là giao điểm của MG và B’C’. Gọi Q là giao điểm của ME và AD. Khi đó mặt phẳng (MNP) chính là mặt phẳng (MEG). Gọi d 1 , d 2 lần lượt là khoảng cách từ C, A đến mặt phẳng (MEG). Do AC cắt (MEG) tại điểm H (như hình vẽ) nên d 1 d 2 = H C H A . Do tứ diện CMEG là tứ diện vuông tại C nên
1 d 1 2 = 1 C M 2 + 1 C E 2 + 1 C G 2
Ta có G C ' G C = C ' N C E = 1 3
Suy ra G C = 3 2 C C ' = 9 a 2
Như vậy: 1 d 1 2 = 1 a 2 + 4 9 a 2 + 4 81 a 2
Từ đó d 1 2 = 81 a 2 12 ⇒ d 1 = 9 11 . Ta có Q D M C = E D E C = 1 3 ⇒ Q D = a 3
Ta có Δ H C M đồng dạng với Δ H A Q nên:
H C H A = M C A Q = a 2 a − a 3 = 3 5 ⇒ d 1 d 2 = 3 5 ⇒ d 2 = 5 3 d 1 = 5.9 a 3.11 = 15 a 11
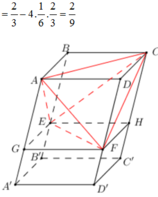
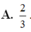
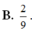
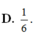
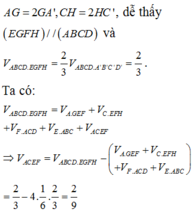
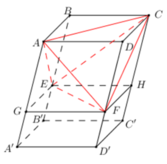
Giả sử (AEF) cắt CC’ tại I. Khi đó ta có AE// FI, AF // EI nên tứ giác AEIF là hình bình hành. Trên cạnh CC’ lấy điểm J sao cho CJ = DF. Vì CJ song song và bằng DF nên JF song song và bằng CD. Do đó tứ giác CDFJ là hình chữ nhật. Từ đó suy ra FJ song song và bằng AB. Do đó AF song song và bằng BJ. Vì AF cũng song song và bằng EI nên BJ song song và bằng EI.
Từ đó suy ra IJ = EB = DF = JC = c/3
Ta có
Nên V H = V A . BCIE + V A . DCIF
Vì thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng abc nên
Từ đó suy ra