Một sợi dây đàn hồi có một đầu cố định, một đầu tự do. Sóng dừng xảy ra trên dây đàn hồi khi
A. chiều dài của dây bằng số nguyên lần nửa bước sóng.
B. chiều dài của dây bằng số nguyên lần bước sóng.
C. chiều dài của dây bằng một phần tư bước sóng.
D. chiều dài của dây bằng một số nguyên lẻ lần một phần tư bước sóng.

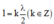
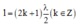
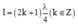
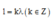

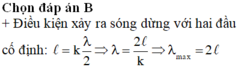
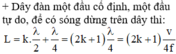
Đáp án: D