Trong các cặp hàm số dưới đây, hàm số nào là nguyên hàm của hàm số còn lại? sin 2 x v à sin sin 2 x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C.
+ Xét hàm y = f(x) = cos 3x
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-3x) = cos 3x = f(x)
Do đó, y = f(x) = cos 3x là hàm chẵn trên tập xác định của nó.
+ Xét hàm y = g(x) = sin (x2 + 1)
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = sin ((-x)2 + 1) = sin (x2 + 1) = g(x)
Do đó: y = g(x) = sin (x2 + 1) là hàm chẵn trên R.
+ Xét hàm y = h(x) = tan2 x
TXĐ: D = R\{π/2 + k2π, k ∈ Z)
Với mọi x ∈ D, ta có: -x ∈ D và h(-x) = tan2 (-x) = tan2 x = h(x)
Do đó: y = h(x) = tan2 x là hàm số chẵn trên D
+ Xét hàm y = t(x) = cot x.
TXĐ: D = R\{kπ, k ∈ Z)
Với mọi x ∈ D, ta có: -x ∈ D và t(-x) = cot (-x) = -cot x = -t(x)
Do đó: y = t(x) = cot x là hàm số lẻ trên D.

Hàm \(y = \cot x\)là hàm tuần hoàn với chu kì \(T = \pi \)do :
- Tập xác định là \(D = R\backslash \left\{ {k\pi ;k \in Z} \right\}\)
- Với mọi \(x \in D\), ta có \(x - \pi \; \in D\) và \(x + \pi \in D\;\)
Suy ra
\(\begin{array}{l}f\left( {x + \pi } \right) = \cot \left( {x + \pi } \right) = \cot \left( x \right) = f(x)\\f\left( {x - \pi } \right) = \cot \left( {x - \pi } \right) = \cot \left( x \right) = f\left( x \right)\end{array}\)

+ Xét hàm số y= f(x) = cos3x
TXĐ: D =R
Với mọi x ∈ D , ta có: - x ∈ D và
f( -x) = cos( - 3x) = cos3x = f(x)
Do đó, y= cos 3x là hàm chẵn trên tập xác định của nó.
+ Xét hàm y= g(x)= sin(x2 + 1)
TXĐ: D= R
Với mọi x ∈ D , ta có: - x ∈ D và
g( -x)= sin[ (-x)2 +1]= sin( x2+1)= g(x)
Do đó: y= sin( x2 +1) là hàm chẵn trên R.
+ Xét hàm số y= h( x)= tan2x .
TXĐ: 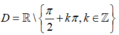
Với mọi x ∈ D , ta có: - x ∈ D và
h( -x)= tan2 (-x)= (- tanx)2 = tan2 x= h(x)
Do đó y= tan2x là hàm số chẵn trên D.
+ Xét hàm số y= t(x)= cotx.
TXĐ: ![]()
Với mọi x ∈ D , ta có: - x ∈ D và t(-x)= cot(-x) = - cotx = - t(x)
Do đó: y= cotx là hàm số lẻ trên D.
Vậy (1); (2); (3) là các hàm số chẵn
Đáp án C

Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).

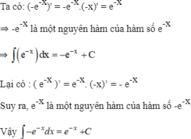
 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số