Một ống thuỷ tinh được cắm lộn ngược vào một chậu chứa thuỷ ngân, bên trong ống chứa 40 c m 3 không khí và một cột thuỷ ngân cao 8 cm so với mực thuỷ ngân trong chậu (H.29.2a). Người ta ấn sâu ống thủy tinh vào thủy ngân cho tới khi mực thủy ngân ở bên trong và bên ngoài ống bằng nhau (H.29.2b). Tính thể tích của không khí còn lại bên trong ống thủy tinh. Biết áp suất khí quyển là 75 cmHg.
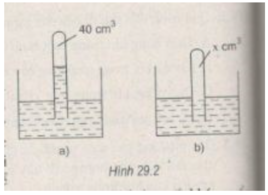

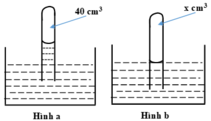
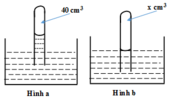
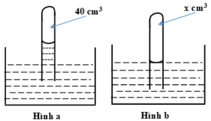

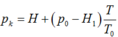
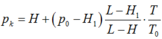
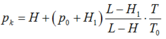
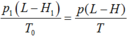

Trạng thái đầu: V 1 = 40 c m 3 ; p 1 = 75 – 8 = 67 cmHg.
Trạng thái cuối: V 2 = ? c m 3 ; p 2 = 75 cmHg.
Vì nhiệt độ không đổi nên: p 1 V 1 = p 2 V 2
⇒ V 2 = p 1 V 1 / p 2 ≈ 35,7( c m 3 )