Cho hình bên, trong đó ABCD là hình bình hành. Chứng minh H và K đối xứng với nhau qua điểm O
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 11 2021
Xét tam giác AHO và tam giác CKO lần lượt vuông tại H và K có:
\(\widehat{AOH}=\widehat{KOC}\)(đối đỉnh)
AO=OC(O là giao điểm 2 đường chéo hình bình hành nên O là trung điểm AC)
=> ΔAHO=ΔCKO(ch-gn)
=> OH=OK
Mà K,O,H thẳng hàng
=> O là trung điểm HK
=> K đx với H qua O
7 tháng 10 2021
a: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=BC
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra:AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
PT
1
CM
30 tháng 1 2019
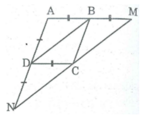
Tứ giác ABCD là hình bình hành:
⇒ AB // CD hay BM // CD
Xét tứ giác BMCD ta có:
BM // CD
BM = CD( = AB ) (gt)
Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ MC // BD và MC = BD (1)
+) Ta có AD // BC (gt) haỵ DN // BC
Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)
Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ CN // BD và CN = BD (2)
Từ (1) và (2) theo tiên đề Ơ- clit suy ra: M, C, N thẳng hàng và MC = CN( = BD).
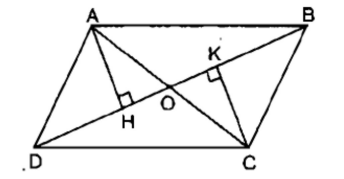
Xét hại tam giác vuông AHO và CKO, ta có:
∠ (AHO)= ∠ (CKO)= 90 0
OA = OC (tính chất hình bình hành)
∠ (AOH)= ∠ (COK)(đối đỉnh)
Suy ra: ∆ AHO = ∆ CKO (cạnh huyền, góc nhọn)
⇒ OH = OK
Vậy O là trung điểm của HK hay điểm H đối xứng với điểm K qua điểm O