Cho các số tự nhiên n, k thỏa mãn 0 ≤ k ≤ n . Trong các đẳng thức sau, đẳng thức nào đúng
![]()
![]()
![]()

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

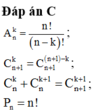

Đáp án C
A n k = n ! n - k ! ; C n + 1 k = C n + 1 n + 1 - k ; C n k + C n k + 1 = C n + 1 k + 1 ; P n = n !

Chọn D
Dựa vào công thức ta có C n k = C n - 1 k - 1 + C n - 1 k

Chọn D
Theo tính chất tổ hợp SGK: C n k - 1 + C n k = C n + 1 k

Nếu m >0 thì – m <0
Ta có: n <0 và – m <0 nên n + (-m) < 0 hay n – m < 0
Chọn B.

Do n^2 là số chính phương nên chia 4 chỉ có thể dư 0 hoặc 1
Mà 2006 chia 4 dư 2 nên k^2 chia 4 chỉ có thể dư 2 hoặc 3, vô lí.
Chứng tỏ không có số n nào thỏa mãn đẳng thức trên.

Gọi I là tâm của hình chữ nhật ABCD ta có 2 M I → = M A → + M C → 2 M I → = M B → + M D → , ∀ M .
Do đó :
M A → + M B → + M C → + M D → = k ⇔ ( M A → + M C → ) + ( M B → + M D → ) = k ⇔ 2 M I → + 2 M I → = k ⇔ 4 M I → = k ⇔ M I → = k 4 . ( * )
Vì I là điểm cố định nên tập hợp các điểm M thỏa mãn đẳng thức (*) là đường tròn tâm I bán kính R = k 4 .
Chọn C.
