Cứu mình với mình cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(A=\sqrt{3-\sqrt{5}}-\sqrt{4-\sqrt{15}}+\sqrt{6-3\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\sqrt{6-2\sqrt{5}}-\sqrt{8-2\sqrt{15}}+\sqrt{12-6\sqrt{3}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}-1-\sqrt{5}+\sqrt{3}+3-\sqrt{3}\right)\)
=2/căn 2=căn 2
\(B=\sqrt{4-\sqrt{7}}-\sqrt{14-5\sqrt{3}}-\sqrt{5+\sqrt{21}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{7}}-\sqrt{28-10\sqrt{3}}-\sqrt{10+2\sqrt{21}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{7}-1-5+\sqrt{3}-\sqrt{7}-\sqrt{3}\right)\)
=-6/căn 2=-3căn2
\(C=\sqrt{11-6\sqrt{2}}-\sqrt{6-4\sqrt{2}}+\sqrt{7-2\sqrt{6}}\)
=3-căn 2-2+căn 2+căn 6-1
=căn 6
\(D=\sqrt{6-\sqrt{11}}-\sqrt{10+3\sqrt{11}}+2\sqrt{2}-1\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12-2\sqrt{11}}-\sqrt{20+6\sqrt{11}}\right)+2\sqrt{2}-1\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{11}-1-\sqrt{11}-3\right)+2\sqrt{2}-1\)
=-1
\(F=\sqrt{6+3\sqrt{3}}-\sqrt{2+\sqrt{3}}+\sqrt{6-4\sqrt{2}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12+6\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)+2-\sqrt{2}\)
=1/căn 2(3+căn 3-căn 3-1)+2-căn 2
=căn 2+2-căn 2
=2

Gấp quá em nhỉ!
A = 2 + 22 + 23 +24 + 25 +....+2200
2A = 22 + 23 + 24 + 25+....+2200 + 2201
2A - A = 2201 - 2
A = 2201 - 2
A = (24)50.2 - 2
A = (\(\overline{...6}\))50.2 - 2
A = \(\overline{...6}\) . 2 - 2
A = \(\overline{...2}\) - 2
A = \(\overline{...0}\) \(\Rightarrow\) A = C . 10 ( C \(\in\) N*)
Thay A = C .10 vào biểu thức B = -1,9 . A ta có :
B = -1,9 . C .10
B = -(1,9 .10) .C
B = - 19.C vì C \(\in\) N \(\Rightarrow\) B \(\in\) Z (đpcm)

a: \(f\left(x\right)=-x^4-8x^3+5x^2+6x-7\)
\(g\left(x\right)=x^4+8x^3-5x^2+5\)
b: \(f\left(x\right)+g\left(x\right)=6x-2\)
\(f\left(x\right)-g\left(x\right)=-2x^2-16x^3+10x^2+6x-12\)
c: |x|=1 thì x=-1 hoặc x=1
h(-1)=6x(-1)-2=-8
h(1)=6x1-2=4
a/ với f(x)
có : \(-x^4-8x^3+5x^2+6x-7\)
với g(x)
có :\(x^4+8x^3-5x^2+5\)
b, f(x) \(-x^4-8x^3+5x^2+6x-7\)
g(x) \(x^4+8x^3-5x^2\) + 5
f(x)+g(x) = 6x-2




1: Để C là số nguyên thì 2n+2-3 chia hết cho n+1
=>\(n+1\in\left\{1;-1;3;-3\right\}\)
=>\(n\in\left\{0;-2;2;-4\right\}\)


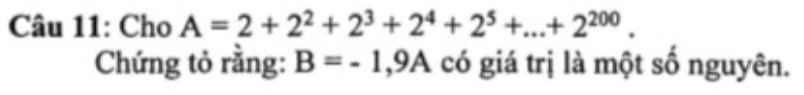


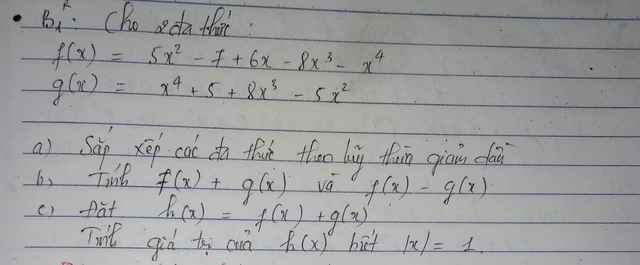




\(\dfrac{1}{-2x^2+4x-2}=\dfrac{x-2}{-2\left(x-1\right)^2\left(x-2\right)}\\ \dfrac{1}{2x^2-6x+4}=\dfrac{x-1}{2\left(x-1\right)^2\left(x-2\right)}\)
rồi cái nào đúng hả bạn