Bài 2: Cho hình vẽ , biết AB = CD, AD = CB
a) Chứng minh: △ABC = △CDA
b) Chứng minh: AB // CD và AD // BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 11 2021
b: Xét tứ giác ABCD có
AB=CD
AD=BC
Do đó: ABCD là hình bình hành
Suy ra: AB//CD;AD//BC
29 tháng 6 2016
ta có : AB//CD và AD//BC
=> ABCD là hình bình hành
=>theo tính chất hình bình hành thì AB=CD VÀ BD = AD
B) nếu O là giao hai đường chéo thì mới làm dduocj
theo tính chất hình bình hành thì hai đường chéo giao nhau tại trung điểm mỗi đường
=> OC=OA và OB=OD
13 tháng 11 2021
b: Xét tứ giác ABCD có
AD//BC
AD=BC
Do đó: ABCD là hình bình hành
Suy ra: BA//CD
Cho hình vẽ A B
Chứng minh: AOB= OCD
Chứng minh: AB=CD VÀ AB//CD
Chứng minh: AD=BC VÀ AD//BC O
11 tháng 12 2021
b: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó:ABCD là hình bình hành
Suy ra: AD=BC
CM
1 tháng 11 2017
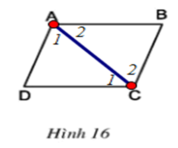
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
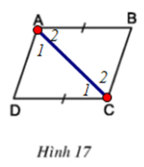
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
KT
3 tháng 8 2018
tự vẽ hình
a) Xét tam giác DAC và tam giác BCA có:
góc DAC = góc BCA (slt do AD // BC)
AC: chung
góc DCA = góc BAC (slt do AB // DC)
suy ra: tam giác DAC = tam giác BCA (g.c.g)
=> AD = BC; DC = AB
b) Xét tam giác DAC và tam giác BCA có:
AD = AB
góc DCA = góc BAC (slt do AB // CD)
AC: chung
suy ra: tam giác DAC = tam giác BCA (c.g.c)
=> AD = BC
góc DAC = góc BCA
mà 2 góc này slt
=> AD // BC