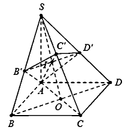
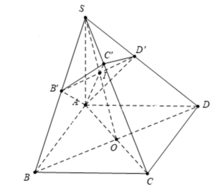
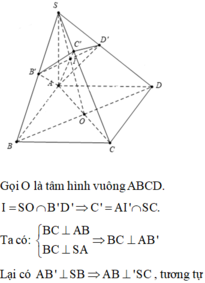
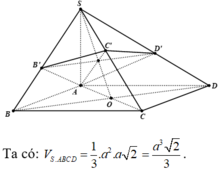
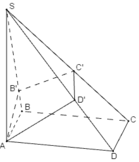
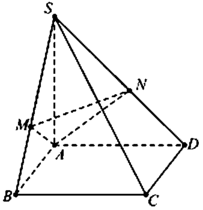
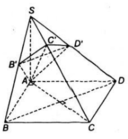
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Gọi B’, D’ là hình chiếu của A lần lượt trên SB, SD. Mặt phẳng (AB’D’) cắt SC tại C’. Thể tích khối chóp S.AB’C’D’ là
A. V = 2 a 3 3 3
B. V = 2 a 3 2 3
C. V = 2 a 3 3 9
D. V = a 3 3 9

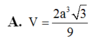
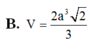
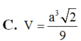
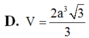

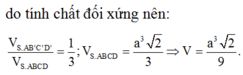

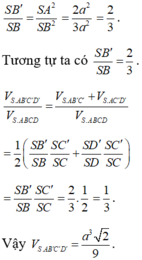



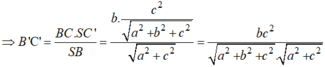
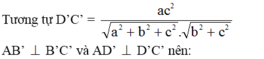 S
∆
A
B
'
C
'
=
1
2
B
'
C
'
.
A
B
'
=
1
2
.
c
2
a
2
+
c
2
.
b
a
2
+
b
2
+
c
2
.
c
a
a
2
+
c
2
S
∆
A
B
'
C
'
=
1
2
B
'
C
'
.
A
B
'
=
1
2
.
c
2
a
2
+
c
2
.
b
a
2
+
b
2
+
c
2
.
c
a
a
2
+
c
2
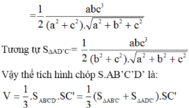
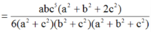



Chọn D