Cho hình chữ nhật ABCD có AB=a, AC=2a. Tính diện tích xung quanh của hình trụ nhận được khi quay hình chữ nhật quanh cạnh AB
A. a 2 2 3 3
B. 3 a 2
C. 2 3 a 2
D. 2 3 π a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Khi quay hình chữ nhật xung quanh cạnh AB thì bán kính hình trụ lúc này R 1 = A D , chiều cao bằng h 1 = A B . Khi đó V 1 = π R 1 2 h 1 = π . A D 2 . A B .
Khi quay hình chữ nhật xung quanh cạnh AD thì bán kính hình trụ lúc này là R 2 = A B , chiều cao h 2 = A D . Khi đó V 2 = π R 2 2 h 2 = π A B 2 . A D .
Do đó, tỉ số thể tích là V 1 V 2 = π . A D 2 . A B π . A B 2 . A D = A D A B = 3 2 .

Khi quay hình chữ nhật ABCD quanh đường AB thì được hình trụ có
R=BC=a, h=AB=2a
\(S_{XQ}=2\cdot pi\cdot a\cdot2a=4\cdot pi\cdot a^2\)

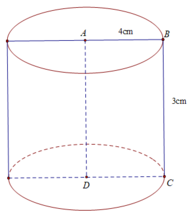
a) Diện tích xung quanh của hình trụ bằng:
S x q = 2πRh = 2π.4.3 = 24π ( c m 2 )

Đáp án B
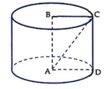
Khi quay đường gấp khúc BCDA quanh trục AB, ta được một hình trụ có bán kính đáy
R = B C = A C 2 − A B 2 = a 5 2 − a 2 = 2 a
chiều cao h = A B = a .
Diện tích xung quanh của hình trụ là: S x q = 2 π R h = 2 π .2 a . a = 4 π a 2