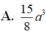
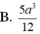
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có S C D N M = S A B C D - S A M N - S B N C
⇒ V S . C D N M = 1 3 . S C D N M . S H = 5 a 2 12
Vì S H ⊥ A B C D nên
V S . C D M N = 1 3 S H . S . C D M N = 1 3 S H . S A B C D - S B C M - S A M N = 1 3 a 3 5 8 a 2 = 5 3 24 a 3
Đáp án B
Đáp án C
Rễ thấy Δ C D N = Δ D A M ⇒ D C N ^ = A D M ^
mà C D H ^ + M D H ^ = 90 0 ⇒ C D H ^ + D C H ^ = 90 0 ⇒ C H ⊥ D H
mà C H ⊥ S H do S H ⊥ A B C D ⇒ D H ⊥ S C H .
Như vậy kẻ H K ⊥ S C thì HK là đường vuông góc chung của DM và SC hay HK là khoảng cách cần xác định.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
C D 2 = C H . C N ⇒ C H = C D 2 C N = C D 2 C D 2 + D N 2 = 4 a 2 4 a 2 + a 2 = 2 a 5
1 H K 2 = 1 S H 2 + 1 C H 2 = 1 9 a 2 + 5 16 s 2 = 61 144 a 2 ⇒ H K = 12 a 61 61
Đáp án B