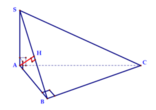
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = A , B C = A 3. Biết rằng SA vuông góc với mặt phẳng đáy và diện tích xung quanh của khối chóp S.ABC bằng 5 a 2 3 2 . Tính theo a khoảng cách d từ A đến mặt phẳng (SBC) gần với giá trị nào nhất sau đây ?
A. 0,72 a
B. 0,90a
C. 0,80a
D. 1,12a

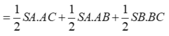
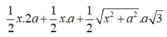
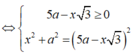
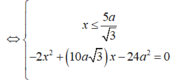
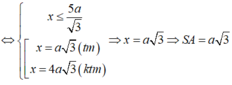
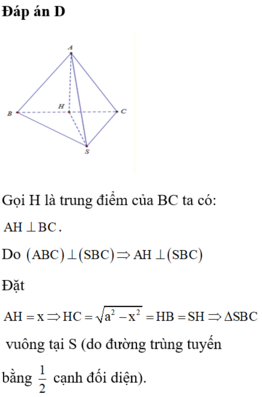

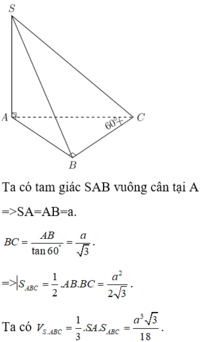


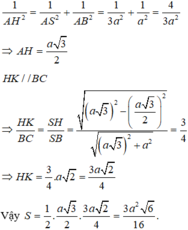
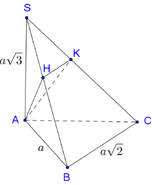
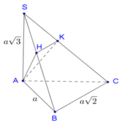


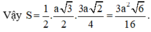
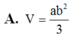
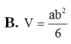
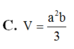
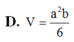

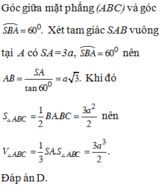
Đáp án B