Vẽ hai đường thẳng cắt nhau sao cho các góc tạo thành có 1 góc bằng 470. Tính số đo các góc còn lại không kể góc bẹ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng 4 góc là 360 độ. Một nửa số đó là 180 độ. Góc còn lại là: 180 - 47 = 133 (độ). Ta có hình vẽ:

Vẽ hình:
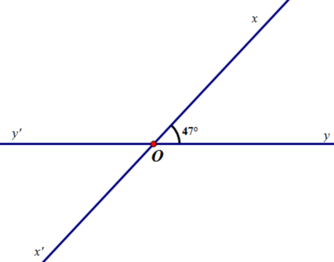
Vẽ đường thẳng xx’.
Trên đường thẳng xx’ ta lấy điểm O bất kì.
Sử dụng thước đo góc để vẽ tia yy’ đi qua O sao cho góc xOy = 47º.
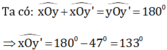
Nhận xét: Ox là tia đối của tia Ox’; Oy là tia đối của tia Oy’ suy ra:
+ hai góc xOy và x’Oy’ là hai góc đối đỉnh nên 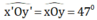
+ hai góc xOy’ và x’Oy là hai góc đối đỉnh nên 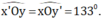
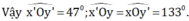

Gỉa sử 2 đường thẳng AD và BD cắt nhau tại O
Gọi góc AOC là góc có số đo bằng 150o, ta có, vì góc AOC và góc BOD là 2 góc đối đỉnh, nên AOC=BOD=150o
Ta có AOC+AOB=180o(hai góc kề bù)
=>150o+AOB=180o
=>AOB=180o-150o=30o
Ta lại có AOB và COD là 2 góc đối đỉnh=>COD=30o

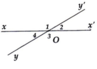
Ta có:
O2 =O4 = 47 độ( đối đỉnh)
Ta có:
O3+O4 = 180 độ ( kề bù)
=> O3 = 180 độ - O4
O3 = 180 độ - 47 độ
O3 = 133 độ
=> O1 = O3 = 133 độ( đối đỉnh)

Giả sử hai đường thẳng \(xx'\)và \(yy'\)cắt nhau tại O và \(\widehat{xOy}=47^0\)
\(\Rightarrow\widehat{x'Oy'}=\widehat{xOy}=47^0\)đối đỉnh
\(\widehat{xOy'}=180^0-\widehat{xOy}=180^0-47^0=133^0\)
do \(\widehat{xOy}\)và \(\widehat{xOy'}\)kề bù và \(\widehat{x'Oy}=\widehat{xOy'}=133^0\)
Bài 2 : Ta có hình vẽ :
Các cặp góc bằng nhau là : \(\widehat{xOy}=\widehat{x'Oy'};\widehat{yOz}=\widehat{y'Oz'}\)

Theo đề bài :
và
đối đỉnh, suy ra :
Ta có và
kề bù suy ra:
+
= 1800
= 1800 -
= 1800 - 470 = 1330
Mà : và
đối đỉnh, suy ra :
=

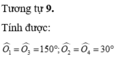
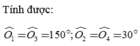
Mk làm rồi :)