Có tất cả bao nhiêu số thực m để có duy nhất một số phức z thoả mãn đồng thời hai điều kiện: z - 1 + i = m và z - 1 - 3 i ≤ 13
A. 2
B. 3
C. 4
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

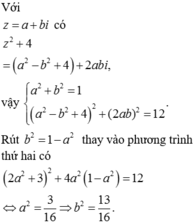
Vậy có 4 cặp (a;b) tức có 4 số phức thoả mãn.
Chọn đáp án D.

Đặt z=x+yi ta có hệ đều kiện:
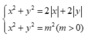
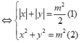
Ta có (1) là tập hợp các cạnh của hình vuông ABCD có tâm là gốc toạ độ độ dài cạnh bằng a = m 2 2 ; là đường tròn (C) có tâm là gốc toạ độ O bán kính bằng R = m.
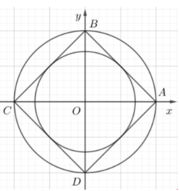
Để có đúng 8 số phức thoả mãn thì (C) phải nằm giữa đường tròn ngoại tiếp và đường tròn nội tiếp hình vuông 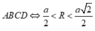
![]()
Chọn đáp án D.

Đáp án A
Đặt z=x+yi
Ta có ![]() suy ra tập biểu diễn số phức z là đường tròn tâm M(0;0) bán kính R=1
suy ra tập biểu diễn số phức z là đường tròn tâm M(0;0) bán kính R=1
![]()
![]() (m > 0) suy ra tập biểu diễn số phức z là đường tròn tâm N(
3
;1) bán kính r=m
(m > 0) suy ra tập biểu diễn số phức z là đường tròn tâm N(
3
;1) bán kính r=m
Để tồn tại duy nhất số phức z thì 2 đường tròn phải tiếp xúc với nhau suy ra MN=R+r![]()
Vậy tập S chỉ có 1 giá trị của m
Gọi M(z) có M thuộc đường tròn
C
1
có tâm
M thuộc đường tròn
C
1
có tâm 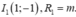
Và thuộc hình tròn
C
2
có tâm
thuộc hình tròn
C
2
có tâm 
Yêu cầu bài toán tương đương với C 1 C 2 có đúng một điểm chung
TH1: C 1 C 2 tiếp xúc ngoài như hình vẽ:
TH2: C 1 C 2 tiếp xúc trong như hình vẽ
Vậy có hai giá trị của tham số.
Chọn đáp án A.