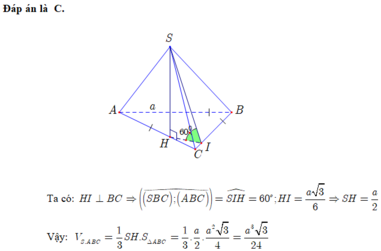
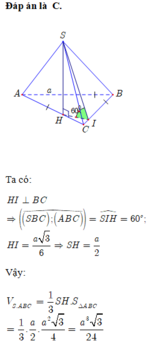
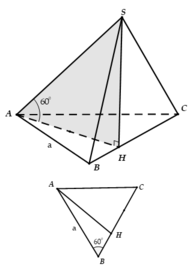
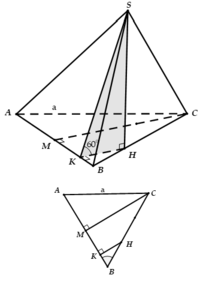
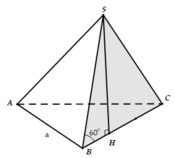
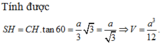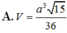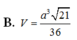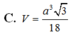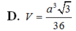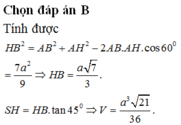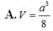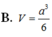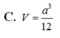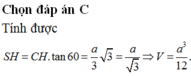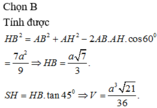Cho hình chóp S . A B C có đáy là tam giác đều cạnh a , hình chiếu vuông góc của đỉnh S trên đáy là điểm H nằm trên cạnh AC sao cho A H = 2 3 A C , mặt phẳng (SBC) tạo với đáy một góc 60 0 .Tính thể tích khối chóp S.ABC
A. a 3 3 12
B. a 3 3 36
C. a 3 3 24
D. a 3 3 8