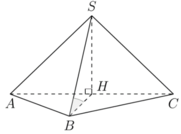
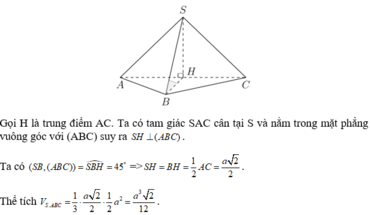
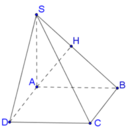
Cho hình chóp S . A B C D có đáy A B C D là hình vuông, tam giác S A B cân tại S . Góc giữa mặt bên S A B và mặt đáy bằng 60 0 , góc giữa S A và mặt đáy bằng 45 0 . Biết thể tích khối chóp S . A B C D bằng 8 a 3 3 3 . Chiều cao của hình chóp S . A B C D bằng
A. a 3 .
B. a 6 .
C. a 3 3 .
D. a 2 3 .


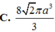
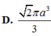



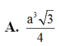


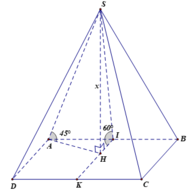

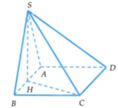
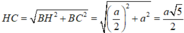
Đáp án A