Trong không gian Oxyz, cho hai điểm A(5;0;0), B(3;4;0). Với C là điểm nằm trên trục Oz, gọi H là trực tâm của tam giác ABC. Khi C di động trên trục Oz thì H luôn thuộc một đường tròn cố định. Bán kính đường tròn đó là
A. 5 4
B. 3 2
C. 5 2
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Đường thẳng AB đi qua điểm B(3;-5;2) và có vectơ chỉ phương là AB → . Vậy phương trình chính tắc của đường thẳng AB là:
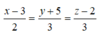

Đáp án C
Đường thẳng AB đi qua B(3; -5; 2) và VTCP AB→(2; -3; 2) có phương trình tham số là:
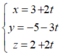

Chọn đáp án B
Gọi I là trung điểm AB và (P) là mặt phẳng trung trực của AB.

Ta có I là trung điểm AB nên I(-1;1;-2)
Lại có A B ⇀ = 4 ; - 8 ; - 6 và A B ⊥ P nên mặt phẳng (P) có một vectơ pháp tuyến là n ⇀ = 2 ; - 4 ; - 3 .
Phương trình mặt phẳng:
![]()
![]()

Mặt phẳng đi qua điểm A(5;-4;2) và nhận A B ⇀ = - 4 ; 6 ; 2 / / 2 ; - 3 ; - 1 làm vectơ pháp tuyến có phương trình là
2 ( x - 5 ) - 3 ( y + 4 ) - ( z - 2 ) = 0 ⇒ 2 x - 3 y - z - 20 = 0
Chọn đáp án A.
Đáp án là A