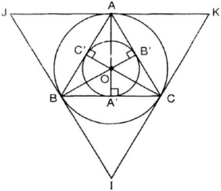
BÀI 30Cho D ABC nội tiếp đường tròn (O; R) có đường cao AH. Gọi I và K lần lượt là hình chiếu của A lên các tiếp tuyến tại B và C của đường tròn (O).
a)Chứng minh 4 điểm A, H, B, I cùng nằm trên một đường tròn b)CMR: AI.AC = AH.AB
c)CMR: AH2= AI.AK
d)Gọi M, N lần lượt là trung điểm của AI và AK. D ABC phải thỏa mãn điều kiện gì để AH = AM + AN


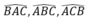
a) Xét tứ giác AHBI có
\(\widehat{AHB}\) và \(\widehat{AIB}\) là hai góc đối
\(\widehat{AHB}+\widehat{AIB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AHBI là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay A,H,B,I cùng nằm trên một đường tròn(đpcm)
b) Xét đường tròn (O; R) có \(\widehat{ABI}=\widehat{ACB}\) (cùng chắc cung AB)
=> \(\widehat{ABI}=\widehat{ACH}\)
Xét ΔABI và ΔACH có: \(\widehat{AIB}=\widehat{AHC}\) (=90o)
\(\widehat{ABI}=\widehat{ACH}\) (cmt)
=> ΔABI ~ ΔACH (g.g) => \(\dfrac{AB}{AC}=\dfrac{AI}{AH}\)=> AI.AC = AH.AB
c) CMTT câu b => ΔABH ~ ΔACK (g.g) => \(\dfrac{AB}{AC}=\dfrac{AH}{AK}\)
=> \(\dfrac{AI}{AH}=\dfrac{AH}{AK}\left(=\dfrac{AB}{AC}\right)\) => AH2 = AI.AK