áp dụng dtsbn:

\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{x+y}{5+2}=\dfrac{-42}{7}=-6\)

\(=>\left\{{}\begin{matrix}x=-30\\y=-12\end{matrix}\right.\)

Áp dụng t/c của dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{x+y}{5+2}=\dfrac{-42}{7}=-6\)

Suy ra: \(\dfrac{x}{5}=-6=>-6.5=-30\)

             \(\dfrac{y}{2}=-6=>-6.2=-12\)

 Vậy \(x=-30;y=-12\)

\(\dfrac{4}{x}=\dfrac{y}{21}=\dfrac{28}{49}=\dfrac{28:7}{49:7}=\dfrac{4}{9}\\ Vậy:x=\dfrac{4.9}{4}=9\\ y=\dfrac{4.21}{9}=\dfrac{28}{3}\)

\(\dfrac{x}{2}=\dfrac{3}{y}\\ \Leftrightarrow x.y=2.3=6\\ Vậy:\left[{}\begin{matrix}\left(x;y\right)=\left(1;6\right)=\left(6;1\right)\\\left(x;y\right)=\left(2;3\right)=\left(3;2\right)\end{matrix}\right.\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{45}{7}\)

Do đó: x=90/7; y=225/7

Áp dụng t/c của dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{45}{7}\)

Khi đó:

\(\dfrac{x}{2}=\dfrac{45}{7}\Rightarrow x=\dfrac{45}{7}.2=\dfrac{90}{7}\)

\(\dfrac{y}{5}=\dfrac{45}{7}\Rightarrow y=\dfrac{45}{7}.5=\dfrac{225}{7}\)

Bài 2: 

Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=k\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=4k\end{matrix}\right.\)

Ta có: xy=12

\(\Leftrightarrow12k^2=12\)

\(\Leftrightarrow k^2=1\)

Trường hợp 1: k=1

\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=3\\y=4k=4\end{matrix}\right.\)

Trường hợp 2: k=-1

\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=-3\\y=4k=-4\end{matrix}\right.\)

Sửa đề câu b) x/3 = y/(-5) và 2x - 3y = -42

a)  Ta có : x/2 = y/3 => x²/4 = y²/9

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

x²/4 = y²/9 = (x²+y²)/(4+9) = 39/13 = 3

=> x²/4 = 3 => x²=12 => x = căn 12

Tương tự ta tìm được y = căn 27

b)  Ta có : x/3 = y/(-5) => 2x/6 = 3y/(-15)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

2x/6 = 3y/(-15) = (2x - 3y) /{6-(-15)} = -42/21 = -2

Từ đó suy ra x = -6,y = 10

a, Ta có: 42 = 2.3.7 = 1.42 = 2.21 = 3.14 = 6.7

Vì a < b nên ta tìm được các cặp số (a ;b) là (1;42), (2;21), (3;14), (6;7)

b, Ta có: 102 = 2.3.17 = 2.51 = 3.34 = 6.17

Vì x; y là số tự nhiên nên x + 5 ≥5 ; y + 2 ≥ 2. Khi đó (x+5)(y+2) = 51.2 = 34.3 = 6.17 = 17.6

Ta có bảng sau:

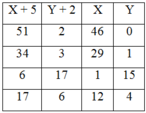
Vậy có các cặp nghiệm (x;y) thỏa mãn đề bài là: (46;0), (29;1), (1;15), (12;4)

1: Áp dụng tính chất của DTSBN, ta được:

\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x-y}{7-13}=\dfrac{42}{-6}=-7\)

=>x=-48; y=-91

2: x/y=3/4

=>4x=3y

=>4x-3y=0

mà 2x+y=10

nên x=3 và y=4

3: =>7x-3y=0 và x-y=-24

=>x=18 và y=42

4: =>7x-5y=0 và x+y=24

=>x=10 và y=14

Áp dụng tính chất của dãy tỉ só bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{t}{5}=\dfrac{x+y+z+t}{2+3+4+5}=\dfrac{-42}{14}=-3\)

Do đó: x=-6; y=-9; z=-12; t=-15

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{t}{5}=\dfrac{x+y+z+t}{2+3+4+5}=\dfrac{-42}{14}=-3\\ \Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-9\\z=-12\\t=-16\end{matrix}\right.\)