Cho điểm E thuộc nửa đường tròn tâm O, đường kính MN=2R. Kẻ tiếp tuyến tại N của nửa đường tròn tân O, tiếp tuyến này cắt đường thẳng ME tại D
Chứng minh tam giác MEN vuông tại E và DE.DM=DN (mũ hai trên đầu DN)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 11 2023
a: Xét (O) có
ΔMEN nội tiếp
MN là đường kính
Do đó: ΔMEN vuông tại E
=>NE\(\perp\)ME tại E
=>NE\(\perp\)DM tại E
Xét ΔDNM vuông tại N có NE là đường cao
nên \(DE\cdot DM=DN^2\)
b: Xét tứ giác ONDI có
\(\widehat{OND}+\widehat{OID}=90^0+90^0=180^0\)
=>ODNI là tứ giác nội tiếp
=>O,D,N,I cùng thuộc một đường tròn
KV
6 tháng 1
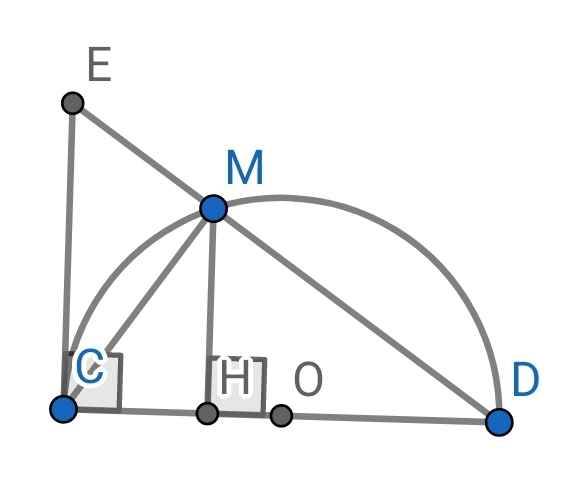a) Do M nằm trên nửa đường tròn đường kính CD (gt)
⇒ ∆DCM vuông tại M
b) Do CE là tiếp tuyến tại C của nửa đường tròn
⇒ CE ⊥ CD
⇒ ∆CDE vuông tại C
Do ∆DCM vuông tại M (cmt)
⇒ CM ⊥ CD
⇒ CM ⊥ DE
⇒ CM là đường cao của ∆CDE
Do ∆CDE vuông tại C, có CM là đường cao
⇒ CD² = MD.ED
⇒ MD.ED = (2r)²
⇒ MD.ED = 4r²
c) ∆DCM vuông tại M, có MH là đường cao
⇒ CH.CD = CM² (1)
∆CDE vuông tại C, có CM là đường cao
⇒ ME.MD = CM² (2)
Từ (1) và (2) ⇒ CH.CD = ME.MD
3 tháng 3 2022
a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
hay ΔCOD vuông tại O
b: Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=MO^2=R^2=AC\cdot BD\)
19 tháng 12 2021
Cho nửa đường tròn đấy ạ . Mn giúp mk với , mk cảm ơn trước ạ 😊😊