Cho đường tròn tâm O . Đường kính AB,CD . Góc BAC = 35độ , bán kính = 5cm
a. Tính chu vi đường tròn . S hình tròn
b.Tính độ dài cung nhỏ BC
c. Tính S hqạt OBmD . Với BmD là cung nhỏ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O) có
CD là dây cung(C,D∈(O))
B là điểm chính giữa của \(\stackrel\frown{CD}\)(gt)
Do đó: \(\stackrel\frown{CB}=\stackrel\frown{BD}\)
⇒\(sđ\widehat{CB}=sđ\widehat{BD}\)(1)
Xét (O) có
\(\widehat{BMD}\) là góc nội tiếp chắn cung BD(gt)
nên \(\widehat{BMD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BD}\)(Định lí góc nội tiếp)(2)
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC(gt)
nên \(\widehat{BAC}=\dfrac{1}{2}\cdot sđ\widehat{CB}\)(Định lí góc nội tiếp)(3)
Từ (1), (2) và (3) suy ra \(\widehat{BMD}=\widehat{BAC}\)(đpcm)

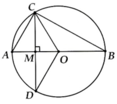
a, AC = 4cm => BC = 4 3 cm
=> R = 4cm => C = 8πcm, S = 16π c m 2
b, ∆AOC đều => A O C ^ = 60 0
=> C O D ^ = 120 0 => l C A D ⏜ = π . 4 . 120 180 = 8 π 3 cm
=> S = 8 π 3 . 4 2 = 16 π 3 c m 2

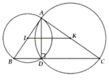
a, A D B ^ là góc nội tiếp trên đường kính AB => A D ⊥ B D
b, Do
A
D
C
^
=
90
0
nên DÎ đường tròn (k;
A
C
2
)
c, ∆IBD cân tại I có B ^ = 60 0 => ∆IBD đều => B I D ^ = 60 0
=> l B D ⏜ = π . 5 2 . 60 180 = 5 6 π cm

* Số đo cung nhỏ AB=góc AOB( góc ở tâm)\(\Rightarrow\) Số đo cung nhỏ AB=60 độ
* Diện ích hình quạt tròn OAB là
\(S=\frac{\pi\times R2\times n}{360}=\frac{\pi\times9\times60}{360}=\frac{3}{2}\pi\approx\frac{3}{2}\times3,14\approx4,71\)cm2
* Số đo cung lớn AB= 360 độ - 60 độ =300 độ
Độ dài cung lớn AB là:
l=3,14*3*300/180=15,7 cm

a, mình chưa hiểu đề lắm
bc, Ta có ^ABC = 300
\(\Rightarrow\widehat{ABC}=\dfrac{1}{2}sđ\stackrel\frown{AC}=50^0\)mà ^AOC là góc ở tâm
\(\Rightarrow\widehat{AOC}=sđ\stackrel\frown{AC}=50^0.2=100^0\)

a: Xet ΔOAC có OA=OC và OA^2+OC^2=AC^2
nên ΔOAC vuôg cân tại O
b: \(BC=\sqrt{AB^2-AC^2}=\sqrt{4R^2-2R^2}=R\sqrt{2}\)
c: ΔOAC vuông cân tại O
=>góc BAC=45 độ
a,C=31,4 S=78,5