Xét tam giác ABC có:

M là trung điểm của AB (GT)

P là trung điểm của BC (GT)

=> MP là đường trung bình tam giác ABC
=> MP = \(\frac{1}{2}\)AC

=> Diện tích MNP = \(\frac{1}{2}\)diện tích ABC 

                              = \(\frac{1}{2}.24\)= 12 (cm²)

Vẽ hình vào nha

a) S_AMC=1/2S_ABC( Vì có đáy MC=1/2 BC và có chung chiều cao hạ từ đỉnh A xuống BC)

=> S_AMC=36:2=18(cm²)

b)* S_ABE=1/2S_ABC( Vì có đáy AE=1/2 AC và có chung chiều cao hạ từ đỉnh B xuống AC)

=> SABE=36:2=18(cm²)

*S_AOE=1/2S_ABE( Vì có đáy OE=1/2 BE và có chung chiều cao hạ từ đỉnh A xuống BE)

=> S_AOE=18:2=9(cm²)

Đáp số: a)18cm²

b)9cm²

@Teoyewmay

Trả lời :

Bạn bấm vào " Câu hỏi tương tự " sẽ có bài giải 

...

Nối AD

+) Xét tam giác ADC đáy DC và tam giác ABC đáy BC  có chung đường cao hạ từ đỉnh A

Vì D là trung điểm AC => \(DC=\frac{1}{2}BC\)

=> \(S_{\Delta ADC}=\frac{1}{2}S_{\Delta ABC}=\frac{1}{2}.560=280\left(m^2\right)\)

 Xét tam giác DFC đáy FC và tam giác DAC đáy AC  có chung đường cao hạ từ đỉnh D

Vì F là trung điểm AC => \(FC=\frac{1}{2}AC\)

=> \(S_{\Delta DFC}=\frac{1}{2}S_{\Delta DAC}=\frac{1}{2}.280=140\left(m^2\right)\)

Tương tự trên mình cũng chứng minh diện tích tam giác AEF= diện tích tam giác BED =140 (m^2)

=> \(S_{\Delta DEF}=S_{\Delta ABC}-S_{\Delta AEF}-S_{\Delta DFC}-S_{\Delta BED}=560-140-140-140=140\left(m^2\right)\)

Từ (1), (2) => \(S_{\Delta DFC}=\frac{1}{2}S_{\Delta DAC}\)=\(\frac{1}{2}.\frac{1}{2}S_{\Delta ABC}=\frac{1}{4}.560=140\)

+) 

Vì M là trung điểm của AB nên:

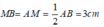
Áp dụng định lí py tago vào tam giác ABC có:

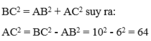
Suy ra: AC = 8cm

Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC nên: MN// AC và

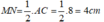
Suy ra: tứ giác MNCA là hình thang vuông.

Diện tích hình thang MNCA là:

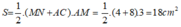
Chọn đáp án D

Tham khảo nhé! Chú ý dòng cuối bị lỗi

Câu hỏi của Trần Đình Thành Đạt - Toán lớp 5 - Học toán với OnlineMath