ĐKXĐ : \(x\ne-5;-m\)

\(\dfrac{x-m}{x+5}+\dfrac{x-5}{x+m}=2\left(1\right)\)

\(\Leftrightarrow\dfrac{\left(x-m\right)\left(x+m\right)+\left(x+5\right)\left(x-5\right)}{\left(x+5\right)\left(x+m\right)}=2\)

\(\Leftrightarrow x^2-m^2+x^2-25=2x^2+2xm+10x+10m\)

\(\Leftrightarrow2xm+10x+m^2+10m+25=0\)

\(\Leftrightarrow2x\left(m+5\right)=-\left(m+5\right)^2\)

\(\Leftrightarrow x=\dfrac{-\left(m+5\right)}{2}\)

PT \(\left(1\right)\) VN \(\Leftrightarrow\left[{}\begin{matrix}\dfrac{-\left(m+5\right)}{2}=-5\\\dfrac{\left(-m+5\right)}{2}=-m\end{matrix}\right.\)

Câu này của bạn có người trả lời lúc trước rồi mà

https://hoc24.vn/cau-hoi/cho-phuong-trinh-an-x-dfracx-mx-5-dfracx-5x-m2-1-voi-nhung-gia-tri-nao-cua-m-thi-phuong-trinh-1-vo-nghiem.377204778288

Phương trình (1):

+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m >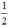 

+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =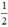 

+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <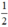 

Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 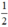; có nghiệm kép khi m =  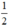và vô nghiệm khi m >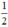 

Lại còn ký tên nữa,sợ bị bản quyền ah=))

a) Phương trình  x 2   –   2 ( m   –   1 ) x   +   m 2   =   0  (1)

Có a = 1; b’ = -(m – 1);  c   =   m 2

b) Phương trình (1):

+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m >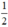 

+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =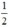 

+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <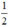 

Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 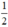; có nghiệm kép khi m =  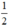và vô nghiệm khi m >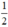 

a: Để đây là phương trình bậc nhất một ẩn thì 3m-2<>0

=>m<>2/3

b: x=-2 là nghiệm của phương trình

=>-2(3m-2)+5=m

=>-6m+4+5-m=0

=>9-7m=0

=>m=9/7

\(\left(3m-2\right)x+5=m\)

\(\Leftrightarrow\left(3m-2\right)x+5=0\)

Để PT trên là bậc nhất một ẩn thì :

\(3m-2\text{≠}0\) \(\Leftrightarrow3m\text{≠}2\Leftrightarrow m\text{≠}\dfrac{2}{3}\)

b) \(\left(3m-2\right)x+5=m\)

\(\Leftrightarrow\left(3m-2\right)\cdot2+5=m\)

\(\Leftrightarrow6m-4+5=m\)

\(\Leftrightarrow5m=-1\)

\(\Leftrightarrow m=\left(-1\right)\div5\)

\(\Leftrightarrow m=-\dfrac{1}{5}\)

Vậy \(m=-\dfrac{1}{5}\) thì phương trình nhận \(x=2\) nghiệm 

a) Thay m=1 vào phương trình, ta được:

\(x^2-6\cdot x+5=0\)

a=1; b=-6; c=5

Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:

\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{5}{1}=5\)

b) Ta có: \(x^2-\left(m+5\right)x-m+6=0\)

a=1; b=-m-5; c=-m+6

\(\Delta=b^2-4ac\)

\(=\left(-m-5\right)^2-4\cdot1\cdot\left(-m+6\right)\)

\(=\left(m+5\right)^2-4\left(-m+6\right)\)

\(=m^2+10m+25+4m-24\)

\(=m^2+14m+1\)

\(=m^2+14m+49-48\)

\(=\left(m+7\right)^2-48\)

Để phương trình có hai nghiệm phân biệt thì \(\left(m+7\right)^2\ge48\)

\(\Leftrightarrow\left[{}\begin{matrix}m+7\ge4\sqrt{3}\\m+7\le-4\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\ge4\sqrt{3}-7\\m\le-4\sqrt{3}-7\end{matrix}\right.\)

Vì x1,x2 là hai nghiệm của phương trình (1) nên ta có:

\(\left\{{}\begin{matrix}x_1^2-\left(m+5\right)x_1-m+6=0\\x_2^2-\left(m+5\right)x_2-m+6=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1^2=\left(m+5\right)x_1+m-6\\x_2^2=\left(m+5\right)x_2+m-6\end{matrix}\right.\)

Ta có: \(x_1^2+x_1\cdot x_2^2=24\)

\(\Leftrightarrow\left(m+5\right)x_1+m-6+x_1\cdot\left[\left(m+5\right)x_2+m-6\right]=24\)

\(\Leftrightarrow\left(m+5\right)x_1+m-6+\left(m+5\right)\cdot x_1x_2+x_1\left(m-6\right)=24\)

Xin lỗi bạn, đến đây mình thua

a, khi m=1

\(=>x^2-6x+5=0\)

\(=>a+b+c=0=>\left[{}\begin{matrix}x1=1\\x2=5\end{matrix}\right.\)

b,\(\Delta=\left[-\left(m+5\right)\right]^2-4\left(-m+6\right)=m^2+10m+25+4m-24\)

\(=m^2+14m+1=m^2+2.7m+49-48\)\(=\left(m+7\right)^2-48\)

pt (1) có nghiệm \(< =>\left(m+7\right)^2-48\ge0\)

\(< =>\left[{}\begin{matrix}m\ge-7+4\sqrt{3}\\m\le-7-4\sqrt{3}\end{matrix}\right.\)

theo vi ét \(=>\left\{{}\begin{matrix}x1+x2=m+5\\x1x2=-m+6\end{matrix}\right.\)

tui nghĩ là đề thế này \(x1^2x2+x1x2^2=24=>x1x2\left(x1+x2\right)=24\)

\(=>\left(6-m\right)\left(m+5\right)=24\)

\(< =>-m^2-5m+6m+30-24=0\)

\(< =>-m^2+m+6=0\)

\(\Delta=1^2-4\left(-1\right).6=25>0\)

\(=>\left[{}\begin{matrix}m1=\dfrac{-1+\sqrt{25}}{2\left(-1\right)}=-2\left(loai\right)\\m2=\dfrac{-1-\sqrt{25}}{2\left(-1\right)}=3\left(tm\right)\end{matrix}\right.\)

a)\(\Delta'=\left[\frac{-2.\left(m-1\right)}{2}\right]^2-m^2=m^2-2m+1-m^2=-2m+1\)

b)Để PT có hai nghiệm phân biệt thì \(\Delta'=-2m+1>0\Rightarrow m<\frac{1}{2}\)

Để PT có nghiệm kép thì: \(\Delta'=-2m+1=0\Rightarrow m=\frac{1}{2}\)

Để PT vô nghiệm thì: \(\Delta'=-2m+1<0\Rightarrow m>\frac{1}{2}\)

\(\Delta'=b'^2-ac\)

p/s b^'=b/2