Trong không gian Oxyz, viết phương trình đường thẳng :
a) Qua hai điểm M (1;0;1) và N (3;2;-1)
b) Qua điểm A (0;-1;3) và song song với đường thẳng chứa hai điểm B (1;0;1) , C (-1;1;2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi H là hình chiếu của A trên đường thẳng d.
Ta có: AH ≤ AM nên khoảng cách từ A đến đường thẳng d nhỏ nhất khi AH trùng với mới AM, khi đó H trùng với M và AM vuông góc d. Mặt phẳng (P) có vecto pháp tuyến n p → (1; 1; 1) . AM → (0; -2; -1) Đường thẳng d nhận vecto [ AM → ; n p → ] làm vecto chỉ phương. Phương trình tham số của d:


Đáp án D.
Ta có A B → = ( 1 ; - 5 ; 4 )
Đường thẳng AB có vecto chỉ phương A B → = ( 1 ; - 5 ; 4 ) nên loại đáp án A, B
Thay tọa độ A(1;2;-3) vào đáp án C được
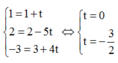
hay điểm A không thuộc đường thẳng ở đáp án C, còn lại đáp án D.
a. \(\overrightarrow{MN}=\left(2;2-2\right)=2\left(1;1;-1\right)\)
Phương trình tham số MN: \(\left\{{}\begin{matrix}x=1+t\\y=t\\z=1-t\end{matrix}\right.\)
b. \(\overrightarrow{BC}=\left(2;1;1\right)\Rightarrow d\) nhận (2;1;1) là 1 vtpt
Phương trình d: \(\left\{{}\begin{matrix}x=2t\\y=-1+t\\z=3+t\end{matrix}\right.\)