Cho ∆ABC vuông tại A. Gọi M, N lần lượt là trung điểm của AB,BC.
a) Chứng minh: AMNC là hình thang vuông
b) Gọi I là trung điểm của AC. Chứng minh: AMNI là hình chữ nhật
c) Tìm điều kiện của ∆ABC đề tứ giác AMNI là hình vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

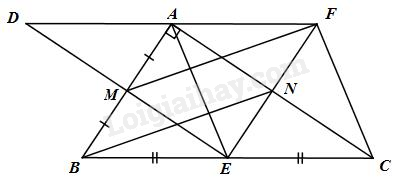
a) \(N\), \(E\) lần lượt là trung điểm của \(AC\) và \(BC(gt)\); Suy ra \(NE\) là đường trung bình của tam giác \(ABC\).
Suy ra \(NE\) // \(AB\)
Suy ra tứ giác \(ANEB\) là hình thang.
Mà \(\widehat {NAB} = 90^\circ \) (do \(\Delta ABC\) vuông tại \(A\))
Do đó tứ giác \(ANEB\) là hình thang vuông.
b) \(M\), \(E\) lần lượt là trung điểm của \(AB\) và \(BC\) (gt);
Suy ra \(ME\) là đường trung bình của \(\Delta ABC\)
Suy ra \(ME\) // \(AC\) hay \(ME\) // \(AN\)
Mà \(AM\) // \(NE\) (do \(AB\) // \(NE\))
Suy ra tứ giác \(AMEN\) là hình bình hành
Mà \(\widehat {{\rm{MAN}}} = 90^\circ \) nên \(AMEN\) là hình chữ nhật
c) Xét tứ giác \(BMFN\) có: \(MF\) // \(BN\) (gt) và \(BM\) // \(FN\) (do \(AB\) // \(NE\))
Suy ra \(BMFN\) là hình bình hành
Suy ra \(BM = FN\)
Mặt khác \(NE = AM\) (Tứ giác \(ANEM\) là hình chữ nhật) và \(AM = BM\)
Suy ra \(FN = NE\)
Tứ giác \(AFCE\) có \(N\) là trung điểm của \(AC\) và \(EF\)
Suy ra \(AFCE\) là hình bình hành
Mà \(AC \bot EF\)
Do đó \(AFCE\) là hình thoi
d) Xét tứ giác \(ADBE\) ta có: \(DE\) và \(AB\) cắt nhau tại \(M\) (gt)
Mà \(M\) là trung điểm của \(AB\) (gt)
\(M\) là trung điểm của \(DE\) (do \(D\) đối xứng với \(E\) qua \(M\))
Suy ra \(ADBE\) là hình bình hành
Suy ra \(AD\) // \(BE\) hay \(AD\) // \(EC\)
Mà \(AF\) // \(EC\) (do \(AECF\) là hình thoi)
Suy ra \(A,D,F\) thẳng hàng (1)
Mà \(ADBE\) là hình bình hành
Suy ra \(BE\) // \(AD\)
Mà \(AF = EC\) (do \(AFCE\) là hình thoi); \(EB = EC\) (gt)
Suy ra \(AD = AF\)(2)
Từ (1) và (2) suy ra \(A\) là trung điểm của \(DF\)

a: Xét ΔABC có
M là trung điểm của BC
E là trung điểm của AC
Do đó: ME là đường trung bình
=>ME//AB và ME=AB/2
hay ME//AH và ME=AH
Xét tứ giác AEMB có ME//AB
nên AEMB là hình thang
mà \(\widehat{EAB}=90^0\)
nên AEMB là hình thang vuông
b: Xét tứ giác MHAE có
ME//AH
ME=AH
Do đó: MHAE là hình bình hành
mà \(\widehat{HAE}=90^0\)
nên MHAE là hình chữ nhật
c: Xét tứ giác BHEM có
ME//BH
ME=BH
Do đó: BHEM là hình bình hành
d: Xét tứ giác BFAM có
H là trung điểm của AB
H là trung điểm của MF
Do đó: BFAM là hình bình hành
mà MA=MB
nên BFAM là hình thoi

a: Xét ΔABC có
M là trung điểm của BC
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//AB
Xét tứ giác ANMB có MN//AB
nên ANMB là hình thang
mà \(\widehat{NAB}=90^0\)
nên ANMB là hình thang vuông
b: Xét tứ giác AMCD có
N là trung điểm của AC
N là trung điểm của MD
Do đó; AMCD là hình bình hành
mà MA=MC
nên AMCD là hình thoi

a: Xét ΔBAC co BM/BA=BN/BC
nên MN//AC và MN=AC/2
=>AMNC là hình thang
mà góc MAC=90 độ
nen AMNC là hình thang vuông
b: Xét tứ giác ANBH có
M là trung điểm chung của AB và NH
NA=NB
nên ANBH là hình thoi

a: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AB
hay AMNB là hình thang
mà \(\widehat{MAB}=90^0\)
nên AMNB là hình thang vuông

a: Xét ΔJVC có
M là trung điểm của JV
N là trung điểm của VC
Do đó: MN là đường trung bình
=>MN//JC
hay JMNC là hình thang vuông

a: Xét tứ giác MBPA có
N là trung điểm của MP
N là trung điểm của BA
Do đó: MBPA là hình bình hành

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
SUy ra: MN//AC
hay AMNC là hình thang vuông
Cho ∆JVC vuông tại J. Gọi M, N lần lượt là trung điểm của JV, VC.
a) Chứng minh: JMNC là hình thang vuông. b) Gọi I là trung điểm của JC. Chứng minh: JMNI là hình chữ nhật c) Tìm điều kiện của ∆JVC để tứ giác JMNI là hình vuônggiải giúp mình nhe