Cho tam giác ABC vuông tại A có BC=5cm. Gọi M,N lần lượt là trung điểm của AB và AC. Khi đó, độ dài MN là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tam giác ABC có:
M là trung điểm AB(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
=> MN//AC
Mà AC⊥AB(tam giác ABC vuông tại A)
=> MN⊥AB(từ vuông góc đến song song)
b) Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(pytago\right)\)
\(\Rightarrow AC^2=BC^2-AB^2=13^2-12^2=25\Rightarrow AC=5\left(cm\right)\)
Ta có: MN là đường trung bình tam giác ABC
\(\Rightarrow MN=\dfrac{1}{2}AC=\dfrac{1}{2}.5=2,5\left(cm\right)\)

Câu 1:
Vì M,N là trung điểm AB,BC nên MN là đtb tg ABC
Do đó \(MN=\dfrac{1}{2}AC=8\left(cm\right)\)
Câu 2:
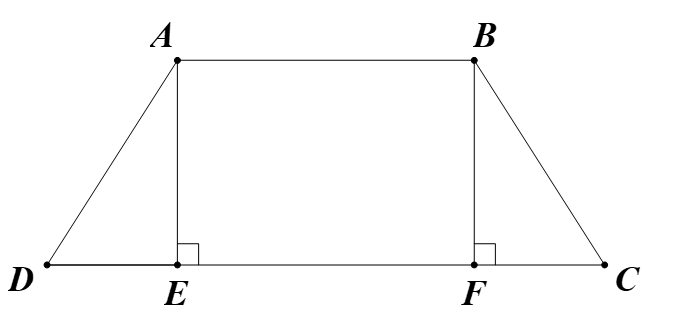
Vì \(\widehat{AEM}=\widehat{AFM}=\widehat{EAF}=90^0\) nên AEMF là hcn

a: Ta có: ΔABC vuông tại A
mà AP là đường trung tuyến
nên \(AP=\dfrac{BC}{2}=5\left(cm\right)\)
Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{1}{2}BC\)
=>\(MN=\dfrac{1}{2}\cdot10=5\left(cm\right)\)
b: Xét ΔABC có
N,P lần lượt là trung điểm của CA,CB
=>NP là đường trung bình của ΔABC
=>NP//AB và \(NP=\dfrac{AB}{2}\)
Ta có: NP//AB
M\(\in\)AB
Do đó: NP//AM
ta có: \(NP=\dfrac{AB}{2}\)
\(AM=\dfrac{AB}{2}\)=MB
Do đó; NP=AM=MB
Xét tứ giác AMPN có
AM//NP
AM=NP
Do đó: AMPN là hình bình hành
Hình bình hành AMPN có \(\widehat{MAN}=90^0\)
nên AMPN là hình chữ nhật

a: AB+BC>AC>AB-BC
=>15>AC>5
=>AC=10(cm)
=>ΔABC cân tại A
b: Xét ΔABN và ΔACM có
AB=AC
\(\widehat{BAN}\) chung
AN=AM
Do đó: ΔABN=ΔACM

a: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
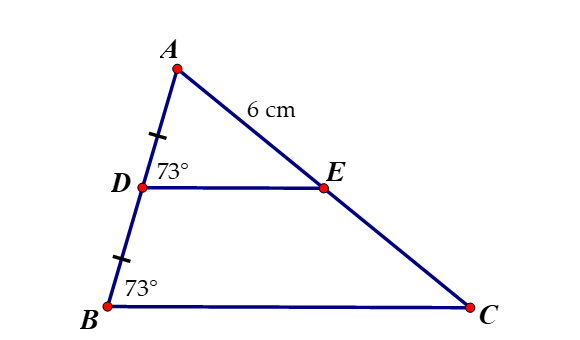
=>MN//BC và \(MN=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
b: Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
Hình thang BMNC có \(\widehat{MBC}=\widehat{NCB}\)
nên BMNC là hình thang cân
c: Ta có: \(MN=\dfrac{BC}{2}\)
mà \(MN=\dfrac{MP}{2}\)
nên BC=MP
Ta có: MN//BC
P\(\in\)MN
Do đó: MP//BC
Xét tứ giác MBCP có
MP//BC
MP=BC
Do đó: MBCP là hình bình hành
Sửa đề: Chứng minh AHCQ là hình chữ nhật
Xét tứ giác AHCP có
N là trung điểm chung của AC và HP
=>AHCP là hình bình hành
Hình bình hành AHCP có \(\widehat{AHC}=90^0\)
nên AHCP là hình chữ nhật
d: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét ΔBAC có
H,M lần lượt là trung điểm của BC,BA
=>HM là đường trung bình của ΔBAC
=>HM//AC và HM=AC/2
Tứ giác AMHC có HM//AC
=>AMHC là hình thang
e:
Ta có: \(HM=\dfrac{AC}{2}\)
\(AN=\dfrac{AC}{2}\)
Do đó: HM=AN
Xét tứ giác AMHN có
HM//AN
HM=AN
Do đó: AMHN là hình bình hành
=>AH cắt MN tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và MN
Ta có: AHCQ là hình chữ nhật
=>AQ//HC và AQ=HC
Ta có: AQ//HC
H\(\in\)BC
Do đó: AQ//HB
ta có: AQ=HC
HB=HC
Do đó: AQ=HB
Xét tứ giác ABHQ có
AQ//BH
AQ=BH
Do đó: ABHQ là hình bình hành
=>AH cắt BQ tại trung điểm của mỗi đường
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN=BC/2=2,5(cm)