Cho điểm A nằm ngoài đường tròn (O;R). Từ A nằm ngoài đường tròn kẻ các tiếp tuyến AB, AC với đường tròn O(B, C là các tiếp điểm). Gọi H là trung điểm của BC và AOa) Chứng minh rằng bốn điểm A, B, C, O cùng thuộc một đường tròn.b) Cho AB = 8cm;BC =9,6cm. Tính bán kính R và số đo góc BAC (làm tròn đến độ)c)Kẻ đường kính BD của đường tròn (O) , AD cắt đường (O) tại điểm thứ 2 là E. Chứng minh góc AHE =...
Đọc tiếp
Cho điểm A nằm ngoài đường tròn (O;R). Từ A nằm ngoài đường tròn kẻ các tiếp tuyến AB, AC với đường tròn O(B, C là các tiếp điểm). Gọi H là trung điểm của BC và AO
a) Chứng minh rằng bốn điểm A, B, C, O cùng thuộc một đường tròn.
b) Cho AB = 8cm;BC =9,6cm. Tính bán kính R và số đo góc BAC (làm tròn đến độ)
c)Kẻ đường kính BD của đường tròn (O) , AD cắt đường (O) tại điểm thứ 2 là E. Chứng minh góc AHE = góc BDE.
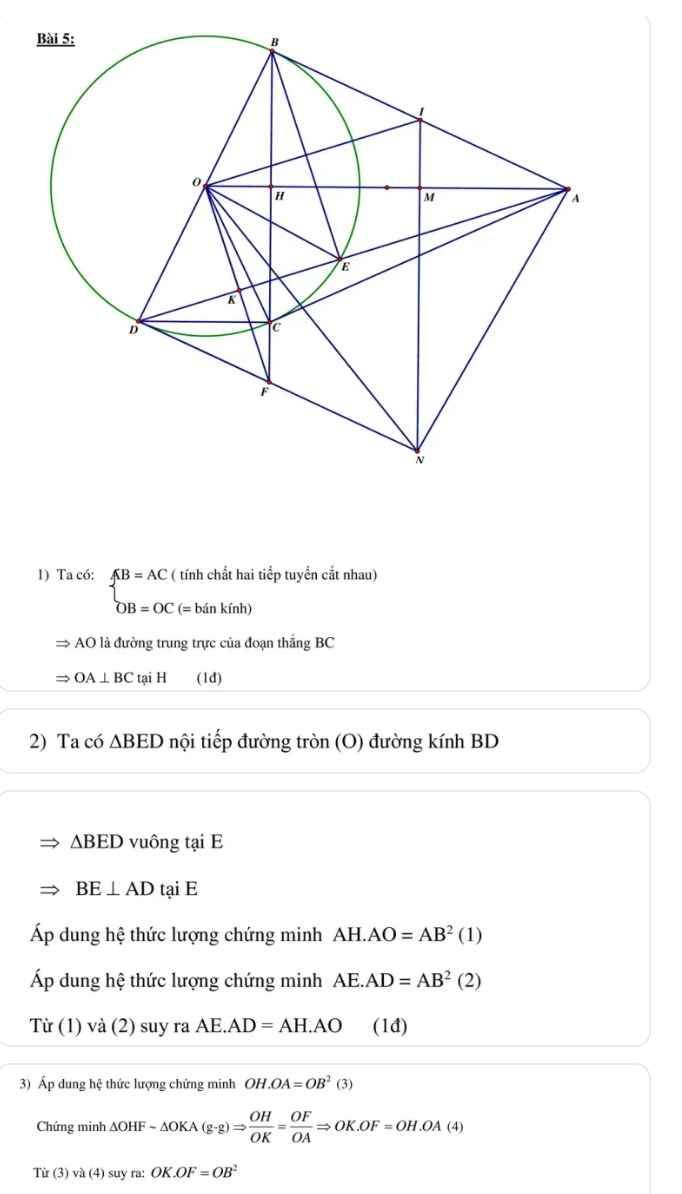
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
c: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)
hay \(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{HAE}\) chung
Do đó: ΔAEH\(\sim\)ΔAOD
Suy ra: \(\widehat{AHE}=\widehat{ADO}=\widehat{BDE}\)