Mọi người có thể giải chi tiết giúp mình câu b và câu c được không, mình mãi không làm được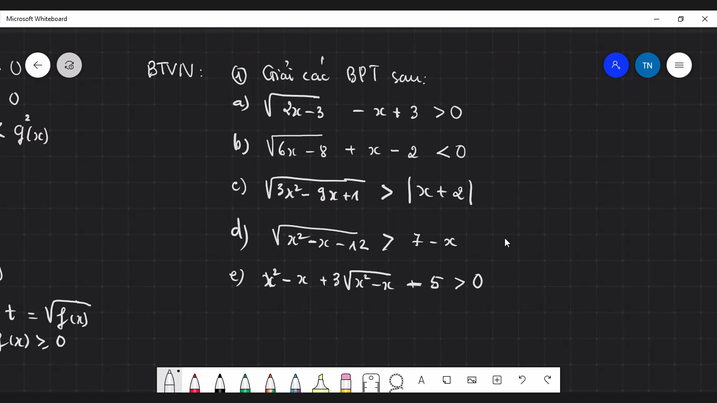
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
const fi='dulieu.dat';
fo='thaythe.out';
var f1,f2:text;
a:array[1..100]of string;
n,d,i,vt:integer;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
n:=0;
while not eof(f1) do
begin
n:=n+1;
readln(f1,a[n]);
end;
for i:=1 to n do
begin
d:=length(a[i]);
vt:=pos('anh',a[i]);
while vt<>0 do
begin
delete(a[i],vt,3);
insert('em',a[i],vt);
vt:=pos('anh',a[i]);
end;
end;
for i:=1 to n do
writeln(f2,a[i]);
close(f1);
close(f2);
end.
Câu 2:
uses crt;
const fi='mang.inp';
fo='sapxep.out';
var f1,f2:text;
a:array[1..100]of integer;
i,n,tam,j:integer;
begin
clrscr;
assign(f1,fi); rewrite(f1);
assign(f2,fo); rewrite(f2);
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
for i:=1 to n do
write(f1,a[i]:4);
for i:=1 to n-1 do
for j:=i+1 to n do
if a[i]>a[j] then
begin
tam:=a[i];
a[i]:=a[j];
a[j]:=tam;
end;
for i:=1 to n do
write(f2,a[i]:4);
close(f1);
close(f2);
end.

đọc lại kĩ đi làm bài 1,2,3 mà làm chắc bài ba

Vì: A, B tác dụng với Na thu số mol H2 bằng 1 nửa tổng số mol A, B.
⇒ A, B là axit đơn chức.
Mà: A, B cộng Br2 thì nBr2 < nA + nB
⇒ A hoặc B có liên đôi C = C trong phân tử.
Gọi: {nCnH2n+1COOH(A)=a(mol)nCmH2m−1COOH(B)=b(mol){nCnH2n+1COOH(A)=a(mol)nCmH2m−1COOH(B)=b(mol)
⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩mA=4,6(g)⇒a=4,614n+46mB=10,32⇒b=10,3214m+44{mA=4,6(g)⇒a=4,614n+46mB=10,32⇒b=10,3214m+44
Mà: a+b=nNaOHa+b=nNaOH
⇒4,614n+46+10,3214m+44=0,22⇒4,614n+46+10,3214m+44=0,22
⇒n=231,84−77,28m43,12m−8,96⇒n=231,84−77,28m43,12m−8,96
Xét từng TH, ta thấy m = 2 thì n = 1 và m = 3 thì n = 0
⇒{A:CH3COOHB:C2H3COOH⇒{A:CH3COOHB:C2H3COOH hoặc {A:HCOOHB:C3H5COOH
học tốt

gọi tổng này là một số A
ta có
A=7/4x(1/1x5+1/5x9+1/9x13+1/13x17+1/17x21)
A= 7/4x(1-1/5+1/5-1/9+1/9-1/13+1/13-1/17+1/17-1/21)
A= 7/4x(1-1/21)=7/4x20/21
suy ra A=5/3
7/1×5 + 7/5x9 + 7/9x13 + 7/13x17 + 7/17x21
= 7/4x(4/1x5 + 4/5x9 + 4/9x13 + 4/13x17 + 4/17x21)
= 7/4x(1 - 1/5 + 1/5 - 1/9 + 1/9 - 1/13 + 1/13 - 1/17 + 1/17 - 1/21)
= 7/4x(1-1/20)
= 7/4x19/20
= 133/80

Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)

Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.

Dạng tổng quát ta càn chứng minh \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{\left(a+b\right)^2}}=\frac{1}{a}+\frac{1}{b}-\frac{1}{a+b}\)
Ta có \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{\left(a+b\right)^2}}\)
\(=\sqrt{\frac{a^4+2a^3b+a^2b^2+2ab^3+b^4}{a^2b^2\left(a+b\right)^2}}\)
\(=\sqrt{\left(\frac{a^2+ab+b^2}{ab\left(a+b\right)}\right)^2}\)
\(=\frac{a^2+ab+b^2}{ab\left(a+b\right)}=\frac{1}{b}+\frac{b}{a\left(a+b\right)}=\frac{1}{b}+\frac{1}{a}-\frac{1}{a+b}\left(đpcm\right)\)
Áp dụng dạng trên ta được
\(D=1+\frac{1}{1}-\frac{1}{2}+1+\frac{1}{2}-\frac{1}{3}+1+\frac{1}{3}-\frac{1}{4}+...+1+\frac{1}{99}-\frac{1}{100}\)
\(D=100-\frac{1}{100}=\frac{9999}{100}\)
Xét biểu thức \(A=\sqrt{1+\frac{1}{a^2}+\frac{1}{\left(a+1\right)^2}}\)với a > 0
\(A^2=1+\frac{1}{a^2}+\frac{1}{\left(a+1\right)^2}=\frac{a^2\left(a+1\right)^2+\left(a+1\right)^2+a^2}{a^2\left(a+1\right)^2}=\frac{a^2\left(a^2+2a+1+1\right)+\left(a+1\right)^2}{a^2\left(a+1\right)^2}=\frac{a^4+2a^2\left(a+1\right)+\left(a+1\right)^2}{a^2\left(a+1\right)^2}=\frac{\left(a^2+a+1\right)^2}{a^2\left(a+1\right)^2}=\left[\frac{a^2+a+1}{a\left(a+1\right)}\right]^2\)Do a > 0 nên A > 0 và \(A=\frac{a^2+a+1}{a\left(a+1\right)}=1+\frac{1}{a\left(a+1\right)}=1+\frac{1}{a}-\frac{1}{a+1}\)
Do đó \(D=\left(1+\frac{1}{1}-\frac{1}{2}\right)+\left(1+\frac{1}{2}-\frac{1}{3}\right)+\left(1+\frac{1}{3}-\frac{1}{4}\right)+...+\left(1+\frac{1}{99}-\frac{1}{100}\right)=99+\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}\right)=100-\frac{1}{100}=99,99\)



 giúp mình giải câu 1 ,2 ,3 và nhớ giải đầy đủ và chi tiết nhé không chi tiết hoặc mấy câu hồi nãy tui nói đó không làm cho vé báo cáo người ta vô coi rạp chiếu phim cho sướng
giúp mình giải câu 1 ,2 ,3 và nhớ giải đầy đủ và chi tiết nhé không chi tiết hoặc mấy câu hồi nãy tui nói đó không làm cho vé báo cáo người ta vô coi rạp chiếu phim cho sướng Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn Mình giải được câu a) và b) rồi . Mọi người giúp c) và d) nhé ! (Ưu tiên gải câu c , không giải câu d cũng được ) Cảm ơn!
Mình giải được câu a) và b) rồi . Mọi người giúp c) và d) nhé ! (Ưu tiên gải câu c , không giải câu d cũng được ) Cảm ơn!