Cho hình bình ABCD có AB = a, BC = b, BD = m và AC = n. Chứng minh rằng m bình phương + n bình phương = 2( a bình phương + b bình phương)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


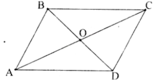
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
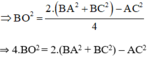
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).

Áp dụng định lí về đường trung tuyến:
OA2 = -
(1)
Thay OA = , AB = a, AD = BC = b và BD = m vào (1) ta có:
\(\left(\dfrac{n}{2}\right)^2=\dfrac{b^2+a^2}{2}-\dfrac{m^2}{4}\)
\(\Leftrightarrow\dfrac{n^2}{4}+\dfrac{m^2}{4}=\dfrac{a^2+b^2}{2}\)
\(\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)

Áp dụng định lí về đường trung tuyến:
OA2 = –
Thay OA = , AB = a
AD = BC = b và BD = m => dpcm


Vì M là trung điểm của AC nên \(AM=\frac{1}{2}AC\)
Áp dụng định lý Pythagoras vào tam giác ABM vuông tại A, ta được:
\(AB^2+AM^2=BM^2\)
hay \(AB^2+\left(\frac{1}{2}BC\right)^2=BM^2\Leftrightarrow AB^2+\frac{1}{4}BC^2=BM^2\)
\(\Leftrightarrow AB^2=BM^2-\frac{1}{4}AC^2\)
Lại áp dụng định lý Pythagoras vào tam giác ABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
hay \(BM^2-\frac{1}{4}AC^2+AC^2=BC^2\)
\(\Leftrightarrow BM^2+\frac{3}{4}AC^2=BC^2\)
\(\Leftrightarrow BM^2=BC^2-\frac{3}{4}AC^2\)
Vậy \(BM^2=BC^2-\frac{3}{4}AC^2\)(đpcm)
Gọi giao điểm của AC và BD là O
Ta có: \(OB^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Leftrightarrow\) \(4OB^2+AC^2=2\left(AB^2+BC^2\right)\)
\(\Leftrightarrow\) \(BD^2+AC^2=2\left(AB^2+BC^2\right)\) (Do \(4OB^2=\left(2OB\right)^2\) mà 2OB = BD)
\(\Leftrightarrow\) \(m^2+n^2=2\left(a^2+b^2\right)\) (đpcm)
Chúc bn học tốt!