Cho hai điểm A,B ở cùng một phía với đường thẳng xy.Tìm trên xy một điểm M sao cho AM và BM làm với đường thẳng xy các góc bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Chỉ cần lấy M,N thuộc hai tia đối nhau Ox và Oy sao cho OM=ON(O là chân đường cao kẻ A xuống xy) thì ta được hai đường xiên AM=AN
b:
Trường hợp 1: D trùng với H thì AD=AH
=>AD>AM
Trường hợp 2: D nằm giữa M và H
=>HD<HM
=>AD<AM(hình chiếu, đường xiên)
Trường hợp 3: D nằm giữa H và N
=>HD<HN
=>AD<AN
mà AM=AN
nên AD<AM

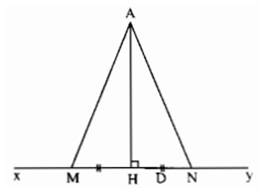
a) Phân tích bài toán: Giả sử M và N là hai điểm của đường thẳng xy mà AM = AN. Nếu gọi H là chân đường vuông góc kẻ từ điểm A đến xy thì HM, HN lần lượt là hình chiếu của các đường xiên AM, AN.
Từ AM = AN suy ra HM = HN, từ đó xác định được hai điểm M, N.
Kẻ AH vuông góc với xy (H ∈ xy)
Lấy hai điểm M, N trên xy sao cho HM = HN (1)
(dùng compa vẽ một đường tròn tâm H bán kính tùy ý; đường tròn này cắt đường thẳng xy tại hai điểm M, N thỏa mãn HM = HN)
Hai đường xiên AM, AN lần lượt có hình chiếu là HM và HN, do đó từ (1) suy ra AM = AN
b) Xét trường hợp D ở giữa M và N
- Nếu D ≡ H thì AD = AH, suy ra AD > AM (đường vuông góc ngắn hơn đường xiên)
- Nếu D ở giữa M và H thì HD < HM, do đó AD < AM (đường xiên có hình chiếu ngắn hơn thì ngắn hơn)
- Nếu D ở giữa H và N thì HD < HN, do đó AD < AN.
Theo a) ta có AM = AN nên AD < AM
Vậy khi D ở giữa M và N thì ta luôn có AD < AM
Lời giải:
a) Giả sử M và N là hai điểm của đường thẳng xy mà AM = AN.
Nếu gọi H là chân đường vuông góc kẻ từ điểm A đến xy thì HM, HN lần lượt là hình chiếu của các đường xiên AM, AN.
Từ AM = AN suy ra HM = HN, từ đó xác định được hai điểm M, N.
Kẻ AH vuông góc với xy (H ∈ xy)
Lấy hai điểm M, N trên xy sao cho HM = HN (1)
(dùng compa vẽ một đường tròn tâm H bán kính tùy ý; đường tròn này cắt đường thẳng xy tại hai điểm M, N thỏa mãn HM = HN)
Hai đường xiên AM, AN lần lượt có hình chiếu là HM và HN, do đó từ (1) suy ra AM = AN
b) Xét trường hợp D ở giữa M và N
- Nếu D ≡ H thì AD = AH, suy ra AD > AM (đường vuông góc ngắn hơn đường xiên)
- Nếu D ở giữa M và H thì HD < HM, do đó AD < AM (đường xiên có hình chiếu ngắn hơn thì ngắn hơn)
- Nếu D ở giữa H và N thì HD < HN, do đó AD < AN.
Theo a) ta có AM = AN nên AD < AM
Vậy khi D ở giữa M và N thì ta luôn có AD < AM

a: Sửa đề: CB
Vì AB và AC là hai tia đốinhau
nên A nằm giữa B và C
mà AB=AC
nên A là trung điểm của BC
b: Vì AC<AM
nênC nằm giữa A và M
mà AC=1/2*AM
nên C là trung điểm của AM

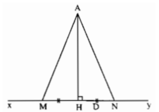
Gọi H là hình chiếu của A trên xy.
Để lấy hai điểm M, N thỏa mãn AM = AN ta vẽ 1 đường tròn tâm A, bán kính > AH cắt đường thẳng xy tại hai điểm M, N.