TÌM X VÀ Y
3x2 +3y2 +6x -12y +15 =0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3x^2+3y^2+6x-12y+15=0\)
\(\Rightarrow3.\left(x^2+y^2+2x-4y+5\right)=0\Rightarrow x^2+y^2+2x-4y+5=0\)
\(\Rightarrow x^2+y^2+2x-4y+1+4=0\)
\(\Rightarrow\left(x^2+2x+1\right)+\left(y^2-4y+4\right)=0\)
\(\Rightarrow\left(x+1\right)^2+\left(y-2\right)^2=0\)
Vì \(\left(x+1\right)^2\ge0;\left(y-2\right)^2\ge0\Rightarrow\left(x+1\right)^2+\left(y-2\right)^2\ge0\)
Mà \(\left(x+1\right)^2+\left(y-2\right)^2=0\)nên để thỏa mãn đẳng thức thì
\(\left(x+1\right)^2=\left(y-2\right)^2=0\) <=> x=-1 và y=2

\(3x^2+3y^2+6x-12y+15=\left(3x^2+6x+3\right)+\left(3y^2-12y+12\right)\)
\(=3.\left(x^2+2x+1\right)+3.\left(y^2-4y+4\right)\)
\(=3.\left(x+1\right)^2+3.\left(y-2\right)^2\)
\(=3.\left(\left(x+1\right)^2+\left(y-2\right)^2\right)\)
\(\Rightarrow3.\left(\left(x+1\right)^2+\left(y-2\right)^2\right)=0\Rightarrow\left(x+1\right)^2+\left(y-2\right)^2=0\)
Mà \(\left(x+1\right)^2\ge0,\forall x\inℝ\)
\(\left(y-2\right)^2\ge0,\forall y\inℝ\)
\(\Rightarrow\left(x+1\right)^2+\left(y-2\right)^2\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)^2=0\\\left(y-2\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x+1=0\\y-2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-1\\y=2\end{cases}}}\)

Điều kiện x ≥ − 7 y ≥ − 1 3 *
x 2 + 2 x y + 8 x = 3 y 2 + 12 y + 9 ( 1 ) x 2 + 4 y + 18 − 6 x + 7 − 2 x 3 y + 1 = 0 ( 2 )
Có 1 ⇔ x 2 + 2 y + 4 x − 3 y 2 − 12 y − 9 = 0 , ta coi (1) là phương trình bậc hai ẩn x và y là tham số, giải x theo y ta được x = − 3 y − 9 x = y + 1
Với x = − 3 y − 9 thì (*) ⇒ − 3 y − 9 ≥ − 7 y ≥ − 1 3 ⇔ y ≤ − 2 3 y ≥ − 1 3 (vô lí)
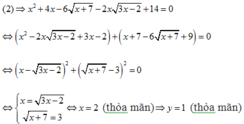
Hệ phương trình có nghiệm là 2 ; 1 ⇒ a = 2 , b = 1 ⇒ T = 24
Đáp án cần chọn là: A

a) x^2 + 4y^2 + 6x - 12y + 18 = 0
<=>x2+6x+9+4y2-12y+9=0
<=>(x+3)2+(2y-3)2=0
<=>x+3=0 và 2y-3=0
<=>x=-3 và y=3/2
b) 5x^2 +9y^2 - 12xy - 6x +9 = 0
<=>x2-6x+9+4x2-12xy+9y2=0
<=>(x-3)2+(2x-3y)2=0
<=>x-3=0 và 2x-3y=0
<=>x=3 và 2.3-3y=0
<=>x=3 và y=2

a/ \(x^2-2.4x+16+y^2+2y+1+z^2=16\Leftrightarrow\left(x-4\right)^2+\left(y+1\right)^2+z^2=16\)
\(\Rightarrow\left\{{}\begin{matrix}I\left(4;-1;0\right)\\R=\sqrt{16}=4\end{matrix}\right.\)
b/ \(x^2+y^2+z^2+2x-y+5z-\dfrac{2}{3}=0\Leftrightarrow x^2+2x+1+y^2-2.\dfrac{1}{2}y+\dfrac{1}{4}+z^2+2.\dfrac{5}{2}z+\dfrac{25}{4}=\dfrac{2}{3}+1+\dfrac{1}{4}+\dfrac{25}{4}\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y-\dfrac{1}{2}\right)^2+\left(z+\dfrac{5}{2}\right)^2=\dfrac{49}{6}\) \(\Rightarrow\left\{{}\begin{matrix}I\left(-1;\dfrac{1}{2};-\dfrac{5}{2}\right)\\R=\dfrac{7}{\sqrt{6}}\end{matrix}\right.\)
P/s: câu c bạn tự làm nốt ạ!

\(3x^2-3y^2-12x+12y\\ =3\left(x^2-y^2\right)-12\left(x-y\right)\\ =3\left(x-y\right)\left(x+y\right)-12\left(x-y\right)\\ =3\left(x-y\right)\left(x+y-4\right)\)
3x2-3y2-12x+12y
=3(x2-y2)-12(x-y)
=3(x-y)(x+y)-4.3(x-y)
=3(x-y)(x+y-4)
\(3x^2+6x+3+3y^2-12y+12=0\)
\(3\left(x^2+2x+1\right)+3\left(y^2-4y+4\right)=0\)
\(3\left(x+1\right)^2+3\left(y-2\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x+1=0\\y-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-1\\y=2\end{cases}}}\)