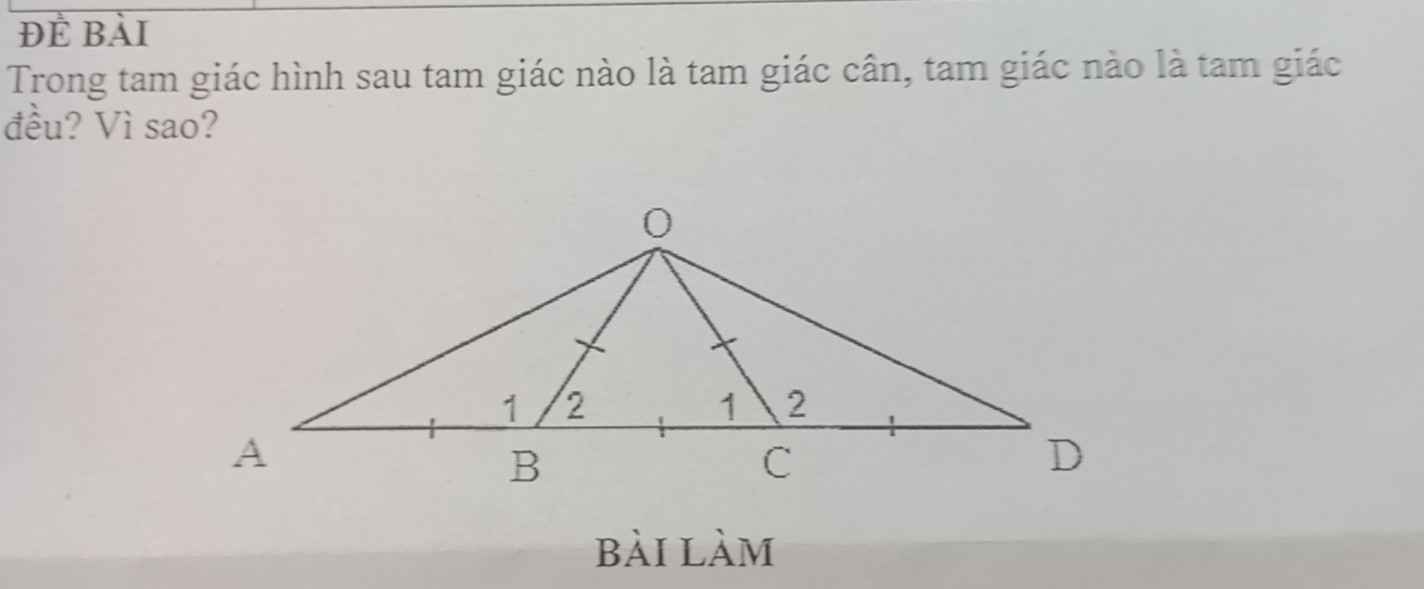
Giúp mình giải với ạ, chi tiết hay ngắn gọn đều được
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì tam giác ABD là tam giác đều
=> DAB = ABD = BDA = 60 độ
=> DA = AB
Vì tam giác AEC là tam giác đều
=> AEC = EAC = ECA = 60 độ
=> AE = AC
=> BAD = CAE = 60 độ
=> BAD + BAC = CAE + BAC
=> CAD = BAE
Xét tam giác AEB và tam giác ADC ta có :
AE = AC
AD = AB
CAD = BAE (cmt)
=> Tam giác AEB = tam giác ADC (c.g.c)
=> DC = BE (dpcm)


Để tìm kiếm người tài giỏi trong thiên hạ một nhà vua đã sai viên quan đi khắp nơi và đưa ra các câu hỏi hóc búa để thử tài nhưng vẫn chưa tìm ra người nào tài giỏi.
Đến cánh đồng thấy hai cha con đang dùng trâu cày đất, viên quan hỏi trâu cày một ngày mấy đường. Cha chưa biết trả lời thế nào thì cậu bé trả lời: nếu như quan trả lời ngựa một ngày đi được bao nhiêu bước thì sẽ cho quan biết trâu cày một ngày được mấy đường. Quan nghe vậy sửng sốt và khẳng định đây là nhân tài,chạy vội về tâu với vua.
Vua thử tài bằng cách bán 3 thùng gạo nếp và 3 con trâu đực dặn nuôi để trong 1 năm ba con trâu đẻ thành chín con. Ai nấy đều lo lắng nhưng cậu bé cứ nói lấy gạo nếp và giết trâu để ăn, còn một phần làm lộ phí cho hai cha con vào kinh. Cậu bé đã chứng minh với nhà vua rằng 3 con trâu đực không thể đẻ.
Nhà vua tiếp tục thử tài cậu bé bằng cách ra lệnh từ một con chim sẻ dọn thành ba cỗ thức ăn. Cậu bé đưa cây kim và nói rằng rèn thành con dao để xẻ thịt chim.
Bây giờ thế lực ngoại bang đe dọa xâm lược, cho người sang thử tài. Cho một vỏ con ốc vặn dài và làm sao để xâu sợi chỉ xuyên qua con ốc đó. Cậu bé nghĩ ra cách lấy con kiến càng buộc chỉ ngang lưng, bên kia thì bôi mỡ để dẫn dụ kiến bò sang. Sợi chỉ được xuyên qua con ốc trong sự ngỡ ngàng, thán phục của sứ giả.
Vua ban thưởng hậu hĩnh cho cậu bé, phong làm trạng nguyên và có việc gì khó cũng đều hỏi ý kiến của cậu bé.

a: \(A=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}\left(x+\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x+\sqrt{x}+1}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)+1=x-\sqrt{x}+1\)
b:
\(\dfrac{x}{12}=\dfrac{\left(\sqrt{5}+2\right)\sqrt[3]{17\sqrt{5}-38}}{\sqrt{5}+\sqrt{14-6\sqrt{5}}}\)
\(\Leftrightarrow x\cdot\dfrac{1}{12}=\dfrac{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}{\sqrt{5}+3-\sqrt{5}}\)
\(\Leftrightarrow\dfrac{x}{12}=\dfrac{1}{3}\)
=>x=36
Khi x=36 thì \(A=36-6+1=37-6=31\)
c: \(B=\dfrac{2\sqrt{x}}{A}=\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}\)
\(B-2=\dfrac{2\sqrt{x}-2x+2\sqrt{x}-2}{x-\sqrt{x}+1}\)
\(=\dfrac{-2x+4\sqrt{x}-2}{x-\sqrt{x}+1}=\dfrac{-2\left(x-2\sqrt{x}+1\right)}{x-\sqrt{x}+1}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}< 0\)
=>B<2
\(2\sqrt{x}>0;x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
=>B>0
=>0<B<2

\(=4\)
Cái này thì bạn rút gọn x - 1 thì còn \(\dfrac{-12}{-3}\)
Sau đó rút gọn -12 và -3 thì chỉ còn 4 thôi
=>(x-1)2 = -12 . (-3)
(x-1)2 = 36
(x-1)2 = 62 = (-6)2
*) x-1=6 *) x-1=-6
x=7 x=-5
=>x thuộc (7,-5)

Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)

a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)



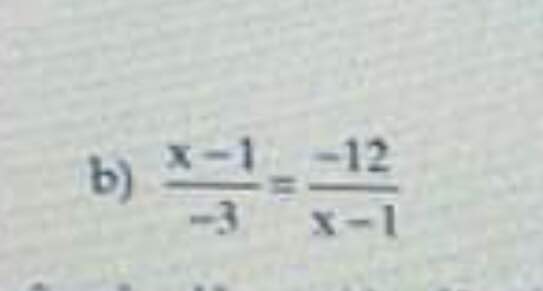
 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn