Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O. AB=a,BD=a căn 3 biết hình chiếu của S lên (ABCD) là điểm M với M là trung điểm OB. Đồng thời SH= a căn3
a) Tính góc giữa (SCD) và (ABCD)
b) Khoảng cách (SD, BC)
c) Khoảng cách (SB,AC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là trung điểm CD
Từ H lần lượt kẻ \(HE\perp SB\) và \(HF\perp SM\)
HM song song AD \(\Rightarrow CD\perp HM\Rightarrow CD\perp\left(SHM\right)\Rightarrow HF\perp\left(SCD\right)\)
\(BC\perp\left(SAB\right)\Rightarrow BC\perp HE\Rightarrow HE\perp\left(SBC\right)\)
\(\Rightarrow\) Góc nhọn giữa HE và HF là góc giữa (SBC) và (SCD)
\(SH=\sqrt{SA^2-AH^2}=a\) \(\Rightarrow\Delta SBH\) vuông cân \(\Rightarrow SE=HE=\dfrac{SB}{2}=\dfrac{a\sqrt{2}}{2}\)
\(HM=BC=a\Rightarrow\Delta SHM\) vuông cân \(\Rightarrow SF=HF=\dfrac{SM}{2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow\dfrac{SF}{SM}=\dfrac{SE}{SB}=\dfrac{1}{2}\Rightarrow EF\) là đường trung bình tam giác SBM
\(\Rightarrow EF=\dfrac{1}{2}BM=\dfrac{1}{2}\sqrt{a^2+a^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow HE=HF=EF\Rightarrow\Delta HEF\) đều
\(\Rightarrow\widehat{EHF}=60^0\) hay góc giữa (SBC) và (SCD) bằng 60 độ
Cách 2:
Ta có \(SH=\sqrt{SA^2-\left(\dfrac{AB}{2}\right)^2}=a\)
Gọi M là trung điểm CD
Đặt hệ trục Oxyz vào chóp với O trùng H, tia Ox trùng tia HB, tia Oy trùng tia HM, tia Oz trùng tia HS
Quy ước a là 1 đơn vị độ dài \(\Rightarrow\) ta có các tọa độ:
\(S\left(0;0;1\right)\) ; \(B\left(1;0;0\right)\) ; \(C\left(1;1;0\right)\) ; \(D\left(-1;1;0\right)\)
\(\Rightarrow\overrightarrow{SB}=\left(1;0;-1\right)\) ; \(\overrightarrow{SC}=\left(1;1;-1\right)\) ; \(\overrightarrow{SD}=\left(-1;1;-1\right)\)
\(\left[\overrightarrow{SB};\overrightarrow{SC}\right]=\left(1;0;1\right)\) \(\Rightarrow\overrightarrow{n_{\left(SBC\right)}}=\left(1;0;1\right)\) là 1 vtpt của (SBC)
\(\left[\overrightarrow{SC};\overrightarrow{SD}\right]=\left(0;2;2\right)=2\left(0;1;1\right)\Rightarrow\overrightarrow{n_{\left(SCD\right)}}=\left(0;1;1\right)\) là 1 vtpt của (SCD)
\(\Rightarrow cos\left[\left(SBC\right);\left(SCD\right)\right]=\dfrac{1.0+0.1+1.1}{\sqrt{1^2+0^2+1^2}.\sqrt{0^2+1^2+1^2}}=\dfrac{1}{2}\)
\(\Rightarrow\left(\left(SBC\right);\left(SCD\right)\right)=60^0\)

Chọn đáp án C
HC là hình chiếu của SC lên mặt phẳng (ABCD).
Góc giữa SC với mặt phẳng (ABCD) là: S C H ^ = 45 °
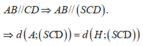
Kẻ 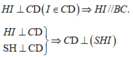
Kẻ 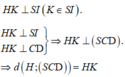
Ta có: ![]()
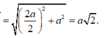
Tam giác SHC vuông cân tại H vì ![]()
Mặt khác: HI = AD = a
Xét tam giác SHI vuông tại H: 
![]()
![]()

Đáp án C
Trong mặt phẳng (ABCD), kẻ DN//CH, dễ thấy AN = AH = HB = SH = a .

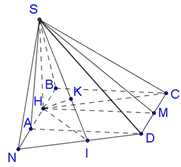
Chắc đề là \(SM=a\sqrt{3}\) vì không có điểm H nào trong dữ liệu
\(BC=AD=\sqrt{BD^2-AB^2}=a\sqrt{2}\)
a.
Qua M kẻ đường thẳng song song BC cắt CD tại E
\(\Rightarrow CD\perp ME\Rightarrow CD\perp\left(SME\right)\)
\(\Rightarrow\widehat{SEM}\) là góc giữa (SCD) và (ABCD)
Áp dụng định lý talet trong tam giác BCD:
\(\dfrac{EM}{BC}=\dfrac{DM}{BD}=\dfrac{3}{4}\Rightarrow EM=\dfrac{3}{4}BC=\dfrac{3a\sqrt{2}}{4}\)
\(\Rightarrow tan\widehat{SEM}=\dfrac{SM}{EM}=\dfrac{2\sqrt{6}}{3}\)
\(\Rightarrow\widehat{SEM}\approx58^031'\)
b.
\(BC||AD\Rightarrow BC||\left(SAD\right)\)
\(\Rightarrow d\left(BC;AD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Lại có: BM cắt (SAD) tại D, mà \(BD=\dfrac{4}{3}MD\)
\(\Rightarrow d\left(B;\left(SAD\right)\right)=\dfrac{4}{3}d\left(M;\left(SAD\right)\right)\)
Trong mp (ABCD), từ M kẻ \(MH\perp AD\)
Trong mp (SMH), từ M kẻ \(MK\perp SH\)
\(\Rightarrow MK\perp\left(SAD\right)\Rightarrow MK=d\left(M;\left(SAD\right)\right)\)
Talet cho tam giác ABD:
\(\dfrac{MH}{AB}=\dfrac{MD}{BD}=\dfrac{3}{4}\Rightarrow MH=\dfrac{3}{4}AB=\dfrac{3a}{4}\)
Hệ thức lượng trong tam giác vuông SMH:
\(MK=\dfrac{SM.MH}{\sqrt{SM^2+MH^2}}=\dfrac{3a\sqrt{19}}{19}\)
\(\Rightarrow d\left(SD;BC\right)=\dfrac{4}{3}MK=\dfrac{4\sqrt{19}}{19}\)