giải phương trình này giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x^2+2}{x^2+4}=0\\ \Leftrightarrow x^2+2=0\)
Ta có: \(x^2\ge0;2>0\Rightarrow x^2+2>0\)
Vậy pt vô nghiệm

Ta có:
(2 - 3x)(x + 8) = (3x - 2)(3 - 5x)
⇔ (2 - 3x)(x + 8) - (3x - 2)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8) + (2 - 3x)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8 + 3 - 5x) = 0
⇔ (2 - 3x)(11 - 4x) = 0
⇔ 2 - 3x = 0 hay 11 - 4x = 0
⇔ 2 = 3x hay 11 = 4x
⇔ x = \(\dfrac{2}{3}\) hay x = \(\dfrac{11}{4}\)
Vậy tập nghiệm của pt S = \(\left\{\dfrac{2}{3};\dfrac{11}{4}\right\}\)
<=> (2-3x ) (x+8) + (2-3x ) (3-5x)=0
<=> (2-3x ) ( x+8 + 3-5x ) =0
<=> (2-3x ) ( 11 - 4x ) = 0
=> 2-3x =0 hoặc 11-4x =0
3x = 2 4x =11
x = 2/3 x = 11/4

\(\Leftrightarrow2cos4x\left(cos2x-sin2x\right)=0\)
\(\Leftrightarrow cos4x=0\) (do \(cos4x=cos^22x-sin^22x\) đã bao hàm \(cos2x-sin2x\))
\(\Rightarrow4x=\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)

để \(\left|8-x\right|=8-x< =>8-x\ge0< =>x\le8\)
\(=>8-x=x^2+x< =>x^2+2x-8=0\)
\(< =>\left(x+1\right)^2-3^2=0< =>\left(x-2\right)\left(x+4\right)=0\)
\(=>\left[{}\begin{matrix}x=2\left(TM\right)\\x=-4\left(TM\right)\end{matrix}\right.\)
*để\(\left|8-x\right|=x-8< =>8-x< 0< =>x>8\)
\(=>x-8=x^2+x< =>x^2=-8\)(vô lí)
vậy x=2 hoặc x=-4

`[x-4]/[x+4]-x/[x-4]=[3x-14]/[x^2-16]` `ĐK: x \ne +-4`
`<=>[(x-4)^2-x(x+4)]/[(x-4)(x+4)]=[3x-14]/[(x-4)(x+4)]`
`=>x^2-8x+16-x^2-4x=3x-14`
`<=>3x+8x+4x=16+14`
`<=>15x=30`
`<=>x=2` (t/m)
Vậy `S={2}`
`(x - 4)/(x + 4) - x/(x - 4) = (3x - 14)/(x^2 - 16)`
`=>` `x = 2`

c: \(12\cdot3^x+3\cdot15^x-5^{x+1}=20\)
=>\(12\cdot3^x+3\cdot3^x\cdot5^x-5^x\cdot5-20=0\)
=>\(3^x\cdot3\left(5^x+4\right)-5\left(5^x+4\right)=0\)
=>\(\left(3^{x+1}-5\right)\left(5^x+4\right)=0\)
=>\(3^{x+1}-5=0\)
=>\(3^{x+1}=5\)
=>\(x+1=log_35\)
=>\(x=log_35-1\)
f: \(25^x-2\left(3-x\right)\cdot5^x+2x-7=0\)
=>\(\left(5^x\right)^2+5^x\cdot\left(2x-6\right)+2x-7=0\)
=>\(\left(5^x\right)^2+5^x\left(2x-7\right)+5^x+2x-7=0\)
=>\(5^x\left(5^x+2x-7\right)+\left(5^x+2x-7\right)=0\)
=>\(\left(5^x+1\right)\left(5^x+2x-7\right)=0\)
=>\(5^x+2x-7=0\)
Đặt \(A\left(x\right)=5^x+2x-7\)
=>\(A'\left(x\right)=5^x\cdot ln5+2>0\forall x\)
=>A(x) đồng biến trên R
=>A(x)=0 khi và chỉ khi x=1
i: \(9^x+2\left(x-2\right)\cdot3^x+2x-5=0\)
=>\(\left(3^x\right)^2+3^x\left(2x-5\right)+3^x+2x-5=0\)
=>\(\left(3^x+2x-5\right)\left(3^x+1\right)=0\)
=>\(3^x+2x-5=0\)
Đặt \(B\left(x\right)=3^x+2x-5\)
=>\(B'\left(x\right)=3^x\cdot ln3+2>0\)
=>B(x) luôn đồng biến trên R
=>B(x)=0 khi và chỉ khi x=1

Lấy \(2.\left(2\right)-\left(1\right)\) ta được:
\(2b+4a+6-\left(a-1-2b\right)=0\)
\(\Leftrightarrow4b+3a+7=0\Rightarrow b=\dfrac{-3a-7}{4}\)
Thế vào (2):
\(\sqrt{a^2+\left(\dfrac{-3a-7}{4}\right)^2}=\dfrac{-3a-7}{4}+2a+3\)
\(\Leftrightarrow\sqrt{25a^2+42a+49}=5a+5\) (\(a\ge-1\))
\(\Leftrightarrow25a^2+42a+49=25a^2+50a+25\)
\(\Rightarrow a=...\Rightarrow b=...\)
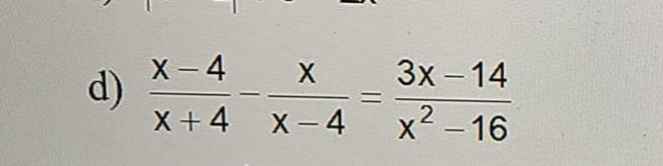
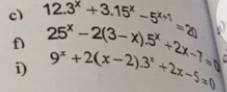

\(\dfrac{1}{a}-\dfrac{a-4}{4a}=6\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\dfrac{4-\left(a-4\right)}{4a}=\dfrac{24a}{4a}\)
\(\Leftrightarrow4-\left(a-4\right)=24a\)
\(\Leftrightarrow4-a+4=24a\)
\(\Leftrightarrow8=25a\)
\(\Leftrightarrow a=\dfrac{8}{25}\left(tm\right)\)
Vậy \(S=\left\{\dfrac{8}{25}\right\}\)