Giúp e bài 7 đi ạ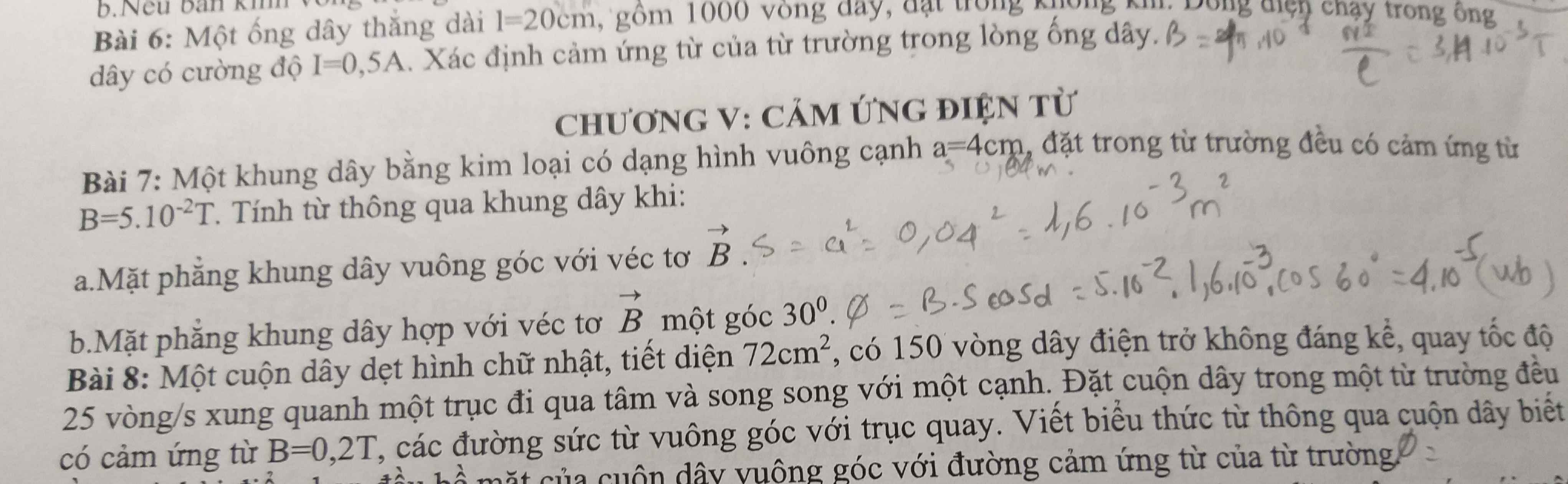
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
(1) \(CH_4+Cl_2\underrightarrow{as}CH_3Cl+HCl\)
(2) \(CH_3Cl+NaOH\underrightarrow{t^o}CH_3OH+NaCl\)
(3) \(CH_3OH+CuO\underrightarrow{t^o}HCHO+H_2O+Cu\)
(4) \(2HCHO+O_2\underrightarrow{t^o,xt}2HCOOH\)
b)
(1) \(CH_3CH_2OH+CuO\underrightarrow{t^o}CH_3CHO+H_2O+Cu\)
(2) \(2CH_3CHO+O_2\underrightarrow{t^o,xt}2CH_3COOH\)
(3) \(CH_3COOH+Na\rightarrow CH_3COONa+\dfrac{1}{2}H_2\)
(4) \(CH_3COONa+NaOH\underrightarrow{t^o,CaO}CH_4+Na_2CO_3\)
c)
(1) \(CH_3CH_2OH\underrightarrow{170^oC,H_2SO_4}CH_2=CH_2+H_2O\)
(2) \(2CH_2=CH_2+O_2\underrightarrow{t^o,xt}2CH_3-CHO\)
(3) \(2CH_3-CHO+O_2\underrightarrow{t^o,xt}2CH_3COOH\)
(4) \(CH_3COOH+C_2H_5OH\underrightarrow{t^o,H_2SO_4}CH_3COOC_2H_5+H_2O\)

a: Xét ΔBEC có BE=BC
nên ΔBEC cân tại B
mà \(\widehat{EBC}=60^0\)
nên ΔBEC đều
b: Xét ΔBEI và ΔBCI có
BE=BC
\(\widehat{EBI}=\widehat{CBI}\)
BI chung
DO đó: ΔBEI=ΔBCI
Suy ra: IE=IC
c: Ta có: ΔBCE cân tại B
mà BI là đường phân giác
nên BI là đường cao
Xét ΔBEC có
BI là đường cao
CA là đường cao
BI cắt CA tại I
Do đó: EI vuông góc với BC
a. Xét Tam giác BEC ta có : BE = BC => Tam giác ABC là tam giác cân
Mà góc B = 60 độ => Tam giác BEC là tam giác đều ( tam giác cân có 1 góc bằng 60 độ là tam giác đều.
b. Xét tam giác BEI và tam giác BCI có :
BI chung
BE = BC
Góc EBI = góc CBI
=> Tam giác BEI = tam giác BCI ( c.g.c)
=> IE = IC (hai cạnh tương ứng)

a.
\(y'=\left(x^2\right)'+\left(4sinx\right)'=2x+4cosx\)
b.
\(y'=\left(2x^3\right)'-\left(sinx\right)'+\left(2\right)'=6x^2-cosx\)
c.
\(y'=\left(5sin\left(x-\dfrac{\pi}{4}\right)\right)'=5.\left(x-\dfrac{\pi}{4}\right)'.cos\left(x-\dfrac{\pi}{4}\right)=5cos\left(x-\dfrac{\pi}{4}\right)\)

a: Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔHAC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF\(\sim\)ΔACB
Suy ra: \(\widehat{AEF}=\widehat{ACB}\)

a.
\(y=x^7\left(x+1\right)=x^8+x^7\)
\(\Rightarrow y'=8x^7+7x^6\)
b.
\(y'=2x+\dfrac{2}{2\sqrt{x}}=2x+\dfrac{1}{\sqrt{x}}\)
c.
\(y'=9x^2+4x\)

\(n_{CH_3COOC_2H_5}=\dfrac{12,3}{88}=\dfrac{123}{880}\left(mol\right)\)
PTHH: CH3COOH + C2H5OH --H2SO4(đ),to--> CH3COOC2H5 + H2O
\(\dfrac{123}{880}\)<----------------------------------\(\dfrac{123}{880}\)
=> \(\%m_{CH_3COOH\left(pư\right)}=\dfrac{\dfrac{123}{880}.60}{12}.100\%=69,89\%\)


a, khi cân bằng nhiệt ta có \(0,5.3,4.10^5+0,5.\left(4200+2100+400\right).t=1.\left(50-t\right).4200\Rightarrow t=5,3^oC\)
b, để nhiệt cân bằng hệ bằng 0 thì lượng nước đá p tan vừa đủ
\(m_đ.3,4.10^5=1.50.4200\Rightarrow m_đ\approx0,617\left(kg\right)\)









Bài 7.
a)Mặt phẳng khung dây vuông góc với vecto \(\overrightarrow{B}\)\(\Rightarrow\left(\overrightarrow{n},\overrightarrow{B}\right)=0^o\)\(\overrightarrow{B}\)\(\overrightarrow{B}\)\(\overrightarrow{B}\)
Từ thông qua khung dây:
\(\Phi=BS\cdot cos\alpha=5\cdot10^{-2}\cdot0,04^2\cdot cos0^o=8\cdot10^{-5}Wb\)
b)Mặt phẳng khung dây hợp với \(\overrightarrow{B}\) một góc \(30^o\Rightarrow\left(\overrightarrow{n};\overrightarrow{B}\right)=60^o\)
Từ thông qua khung dây:
\(\Phi=BS\cdot cos\alpha=5\cdot10^{-2}\cdot0,04^2\cdot cos60^o=4\cdot10^{-5}Wb\)