giúp mik vs mng ưi..
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A = 1 + 3 + 32 + 33 +.... +3100
3A = 3(1 + 3 + 32 + 33 +....+3100)
3A = 3 + 32 + 33 + 34 +....+3101
3A - A = 2A = (3 + 32 + 33 + 34 +.... + 3101) - (1 + 3 + 32 + .... + 3100)
2A = ( 3 - 3 ) + ( 32 - 32) +.....+ (3100 - 3100) + (3101 - 1)
2A = 0 + 0 +....+ 0 + 3101 - 1
2A = 3101 - 1
A = (3101 - 1) : 2

Cái đấy ko thuộc trong chương trình lớp 7 đâu bạn!!Phải các anh chị lớp 8,9 mới giải đc!!!!!

a. Xét tam giác ABD và tam giác HBD có:
góc BAD = góc BHD = 90 độ
BD là cạnh chung
góc ABD = góc HBD ( BD là tia phân giác của góc B)
Vậy tam giác ABD = tam giác HBD ( cạnh huyền - góc nhọn)



2:
a: Xét tứ giác DIHK có
\(\widehat{DIH}=\widehat{DKH}=\widehat{IDK}=90^0\)
Do đó: DIHK là hình chữ nhật
Suy ra: DH=KI(1)
Xét ΔDEF vuông tại D có DH là đường cao ứng với cạnh huyền EF
nên \(DH^2=HE\cdot HF\left(2\right)\)
Từ (1) và (2) suy ra \(IK^2=HE\cdot HF\)

a, Theo tc 2 tt cắt nhau: \(AE=EC;BF=CF\)
Vậy \(AE+BF=EC+CF=EF\)
b, Vì \(\left\{{}\begin{matrix}AE=EC\\\widehat{EAO}=\widehat{ECO}=90^0\\OE.chung\end{matrix}\right.\) nên \(\Delta AOE=\Delta COE\)
\(\Rightarrow\widehat{AOE}=\widehat{EOC}\) hay OE là p/g \(\widehat{AOC}\)
Cmtt: \(\Delta BOF=\Delta COF\Rightarrow\widehat{BOF}=\widehat{COF}\) hay OF là p/g \(\widehat{BOC}\)
Vậy \(\widehat{EOF}=\widehat{COF}+\widehat{COE}=\dfrac{1}{2}\left(\widehat{AOC}+\widehat{BOC}\right)=90^0\) hay OE⊥OF

 giúp e vs ạ mng ưi
giúp e vs ạ mng ưi 
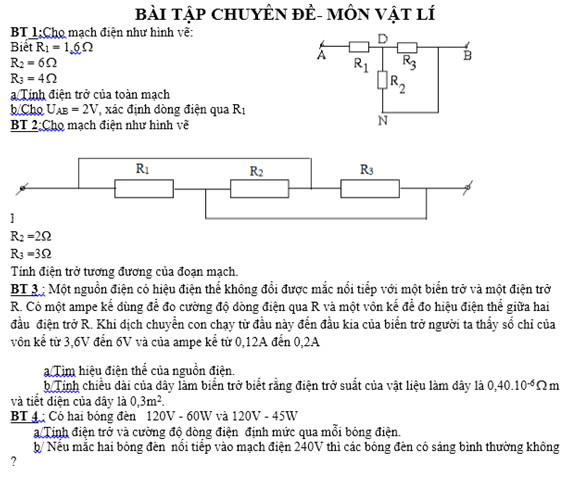 mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.
mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.


2:
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
ΔBAD cân tại B có BE là phân giác
nên BE vuông góc AD
b: Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
c: Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
AF=DC
=>ΔEAF=ΔEDC
=>EF=EC
=>ΔECF cân tại E
d: ΔEAF=ΔEDC
=>góc AEF=góc DEC
=>góc AEF+góc AED=180 độ
=>D,E,F thẳng hàng