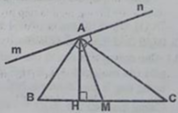
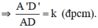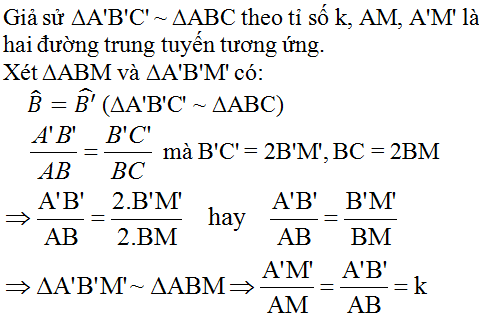Cho tam giác ABC đồng dạng tam giác MNP tương ứng ∠𝐴 = ∠𝑀, ∠𝐵 = ∠𝑁. Kẻ các đường trung tuyến AE và MF của hai tam giác. (𝐸 ∈ 𝐵𝐶; 𝐹 ∈ 𝑁𝑃). a. Chứng minh rằng tam giác AEB đồng dạng tam giác MFN. b. Cho biết tỷ số đồng dạng 𝐴𝐵 𝑀𝑁 = 𝑘. Chứng minh rằng 𝐴𝐸 = 𝑘. 𝑀𝐹.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: ΔABC đồng dạng với ΔMNP
=>AB/MN=BC/NP=AC/MP và góc B=góc N
=>AB/MN=BE/NF và góc B=góc N
Xét ΔABE và ΔMNF có
AB/MN=BE/NF
góc B=góc N
=>ΔABE đồng dạng với ΔMNF
b: ΔABE đồng dạng với ΔMNF
=>AB/MN=AE/MF=k
=>AE=k*MF

a: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
Xét ΔADE có AD=AE
nên ΔADE cân tại A
b: Xét ΔABC có
D là trung điểm của AB
DF//AC
Do đó: F là trung điểm của BC
Xét ΔABC có
D là trung điểm của AB
F là trung điểm của BC
Do đó: DF là đường trung bình
=>DF=AE
mà AE=AD
nên DF=AD
=>ΔADF cân tại D
c: Xét tứ giác ADFE có
DF//AE
DF=AE
Do đó: ADFE là hình bình hành
mà AD=AE
nên ADFE là hình thoi
=>AF⊥DE

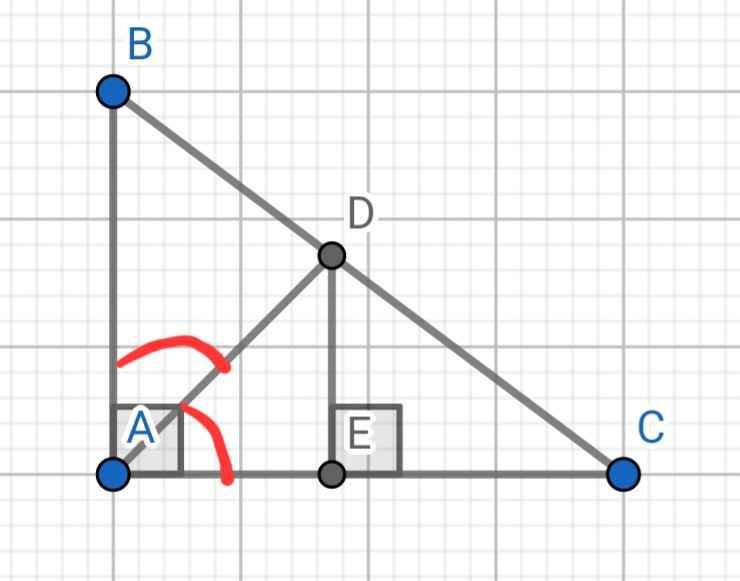
a) Do AD là đường phân giác của ∠BAC
⇒ BD/CD = AB/AC = 9/12 = 3/4
b) Xét hai tam giác vuông: ∆ABC và ∆EDC có:
∠C chung
⇒ ∆ABC ∽ ∆EDC (g-g)
a: BD/CD=AB/AC=3/4
b: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEDC

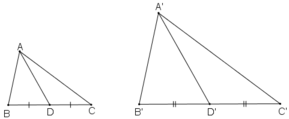
Giả sử ΔA’B’C’  ΔABC theo tỉ số k
ΔABC theo tỉ số k
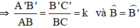
Gọi D, D’ lần lượt là trung điểm BC và B’C’
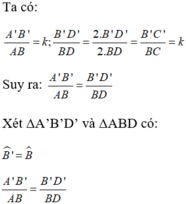
⇒ ΔA’B’D’  ΔABD theo tỉ số k.
ΔABD theo tỉ số k.