Tìm GTNN và GTLN của 2m/(m2+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
\(c,\text{PT có 2 }n_0\text{ phân biệt }\Leftrightarrow\Delta'=2^2-2m>0\Leftrightarrow2m< 4\Leftrightarrow m< 2\)

\(S=\dfrac{2m^2+7m+23}{m^2+2m+10}\Rightarrow Sm^2+2Sm+10S=2m^2+7m+23\)
\(\Leftrightarrow\left(S-2\right)m^2+\left(2S-7\right)m+10S-23=0\)
\(\Delta=\left(2S-7\right)^2-4\left(S-2\right)\left(10S-23\right)\ge0\)
\(\Leftrightarrow4S^2-16S+15\le0\)
\(\Rightarrow\dfrac{3}{2}\le S\le\dfrac{5}{2}\)
\(S_{min}=\dfrac{3}{2}\) khi \(m=-4\)
\(S_{max}=\dfrac{5}{2}\) khi \(m=2\)
Nguyễn Việt Lâm Giáo viên, thầy cho em hỏi tên phương pháp làm của thầy được không ạ??



Đặt \(A=\frac{5-2m}{m^2+2}\Leftrightarrow Am^2+2A-5+2m=0\)
\(\Leftrightarrow Am^2+2m+\left(2A-5\right)=0\)
Để \(PT\) trên có nghiệm \(\Leftrightarrow\Delta'=1-A\left(2A-5\right)=-2A^2+5A+1\ge0\)
\(\Leftrightarrow\frac{5-\sqrt{33}}{4}\le A\le\frac{5+\sqrt{33}}{4}\)
Kết quả ko đẹp lắm nếu cảm thấy sai thì bạn lại đề; mình giải ko sai đâu
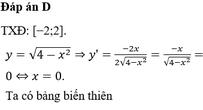
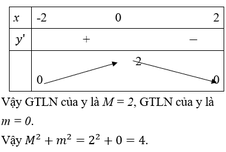
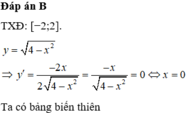

đặt 2m/(m^2+1)=a. nhân chéo lên rùi đưa về dạng pt bậc hai xét denta lớn hơn bằng 0.=>min,mã. OK!