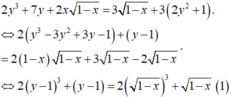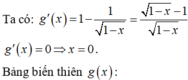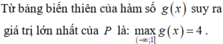Bài làm:

#Tìm Max của biểu thức:

\(A=\frac{3-4x}{x^2+1}=\frac{4\left(x^2+1\right)-\left(4x^2+4x+1\right)}{x^2+1}=4-\frac{\left(2x+1\right)^2}{x^2+1}\)

Mà \(\hept{\begin{cases}\left(2x+1\right)^2\ge0\\x^2+1>0\end{cases}\left(\forall x\right)\Rightarrow}-\frac{\left(2x+1\right)^2}{x^2+1}\le0\left(\forall x\right)\)

\(\Rightarrow A\le4\left(\forall x\right)\)

Dấu "=" xảy ra khi: \(\left(2x+1\right)^2=0\Rightarrow x=-\frac{1}{2}\)

Vậy \(Max\left(A\right)=4\Leftrightarrow x=-\frac{1}{2}\)

#Tìm Max và Min của B:

Tìm Min

\(B=\frac{2x}{x^2+1}=\frac{\left(x^2+2x+1\right)-\left(x^2+1\right)}{x^2+1}=\frac{\left(x+1\right)^2}{x^2+1}-1\)

Mà \(\hept{\begin{cases}\left(x+1\right)^2\ge0\\x^2+1>0\end{cases}\left(\forall x\right)\Rightarrow}\frac{\left(x+1\right)^2}{x^2+1}\ge0\left(\forall x\right)\)

\(\Rightarrow B\ge-1\left(\forall x\right)\)

Dấu "=" xảy ra khi: \(\left(x+1\right)^2\ge0\Rightarrow x=-1\)

Vậy \(Min\left(B\right)=-1\Leftrightarrow x=-1\)

Tìm Max

\(B=\frac{2x}{x^2+1}=\frac{x^2+1-\left(x^2-2x+1\right)}{x^2+1}=1-\frac{\left(x-1\right)^2}{x^2+1}\)

Mà \(\hept{\begin{cases}\left(x-1\right)^2\ge0\\x^2+1>0\end{cases}}\left(\forall x\right)\Rightarrow-\frac{\left(x-1\right)^2}{x^2+1}\le0\left(\forall x\right)\)

\(\Rightarrow B\le1\left(\forall x\right)\)

Dấu "=" xảy ra khi: \(\left(x-1\right)^2=0\Rightarrow x=1\)

Vậy \(Max\left(B\right)=1\Leftrightarrow x=1\)

Sao dạo này nhìu bạn đăng mấy câu như vậy lên thế nhỉ?

b: \(x^2-x+1=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)

c: \(A=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)

Dấu '=' xảy ra khi x=3

d: \(B=-\left(x^2-4x+5\right)=-\left(x^2-4x+4+1\right)=-\left(x-2\right)^2-1\le-1\forall x\)

Dấu '=' xảy ra khi x=2

Đáp án đúng : B

\(A=3yz+\left(4-y-z\right)\left(y+2z\right)\)

\(A=-y^2+4y-2z^2+8z\)

\(A=-\left(y-2\right)^2-2\left(z-2\right)^2+12\le12\)

\(A_{max}=12\) khi \(\left(x;y;z\right)=\left(0;2;2\right)\)

Alooo. Đợt trước anh bảo đợi bảng xếp hạng ổn định rồi tổ chức event jj đó "đền bù" cho box toán mà sao em vừa lót dép ngồi hóng vừa ôn thi mãi từ bấy đến giờ vẫn chẳng thấy đâu zợ?:'(

Đáp án C

P = 4 x y 2 x + x 2 + 4 y 2 P = 4 y x 2 1 + 1 + 4 y x 2 3

Đặt  1 + 4 y x 2 = t , t ≥ 1 ⇒ 4 y x 2 = t 2 − 1

Ta được hàm:

f ( t ) = t 2 − 1 1 + t 3 = t − 1 1 + t 2 , t ≥ 1 f ' ( t ) = − t 2 + 2 t + 3 1 + t 4 f ' ( t ) = 0 ⇔ t = − 1 ( L ) t = 3

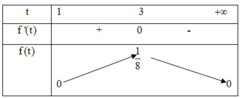
Vậy  max P = max [ 1 ; + ∞ ) f ( t ) = 1 8

\(P-\dfrac{5}{2}=x+2y-\dfrac{x^2+y^2}{2}=-\dfrac{1}{2}\left(x-1\right)^2-\dfrac{1}{2}\left(y-2\right)^2+\dfrac{5}{2}\le\dfrac{5}{2}\)

\(\Rightarrow P-\dfrac{5}{2}\le\dfrac{5}{2}\Rightarrow P\le5\)

\(P_{max}=5\) khi \(\left(x;y\right)=\left(1;2\right)\)

Cảm ơn nhiều ạ !

a) \(A=\dfrac{3}{x-1}\)

Điều kiện \(|x-1|\ge0\)

\(\Rightarrow A=\dfrac{3}{x-1}\ge0\)

\(GTNN\left(A\right)=0\) \(\Rightarrow x-1=+\infty\Rightarrow x\rightarrow+\infty\)

b) \(GTLN\left(A\right)\) không có \(\left(A=\dfrac{3}{x-1}\ge0\right)\)