Giá trị của biểu thức x2-3x2+3x+2 khi x=11
ghi cách làm giùm mình lun nha >,<!!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\frac{3x^2-x+1}{3x+2}=\frac{3x^2+2x-3x-2+3}{3x+2}=\frac{x\left(3x+2\right)-\left(3x+2\right)+3}{3x+2}\)
\(=x-1+\frac{3}{3x+2}\)
Vì x thuộc Z nên x-1 thuộc Z
Vậy A thuộc Z <=> \(\frac{3}{3x+2}\in Z\) <=> 3x+2 là ước của 3
| Ư(2) | 1 | -1 | 3 | -3 |
| 3x+2 | 1 | -1 | 3 | -3 |
| x | -1/3 | -1 | 1/3 | -5/3 |
x thuộc Z nên chọn giá trị x = -1
* Cách làm dạng bài này:
B1: biến đổi mẫu số sao cho chứa ước của tử số
B2: Thu gọn phân số sao cho có phân số mà có tử là số nguyên
B3: Giải

Biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 xác định khi x – 3 ≠ 0,2x + 3 ≠ 0, x 2 - 3 x ≠ 0 và x 2 - 9 ≠ 0
Suy ra: x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ 3 và x ≠ ± 3
Với điều kiện x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3, ta có:
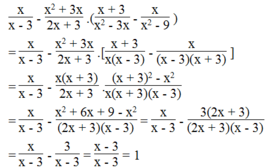
Vậy giá trị của biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 bằng 1 khi x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3

a) \(A=x\left(2x+1\right)-x^2\left(x+2\right)+\left(x^3-x+5\right)\)
\(A=2x^2+x-x^3-2x^2+x^3-x+5\)
\(A=5\)
=> giá trị biểu thức ko phụ thuộc vào biến x
b) \(A=x\left(3x^2-x+5\right)-\left(2x^3+3x-16\right)-x\left(x^2-x+2\right)\)
=> \(A=3x^3-x^2+5x-2x^3-3x+16-x^3+x^2-2x\)
=> \(A=\)16
vậy giá trị của biểu thức A ko phụ thuộc vào biến x

Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)

Bạn à toán tìm cực trị ( tìm GTLN, GTNN, GTTĐ ) ko có trong chương trình toán 6 đâu.
Tìm cực trị chỉ có cách đơn giản nhất như câu trả lời cũ của mình thôi.
Bạn có thể kiểm chứng trên mạng bằng cách gõ: tìm giá trị lớn nhất, giá trị nhỏ nhất

Vì \(x_1\) là nghiệm PT nên \(x_1^2+3x_1-7=0\Leftrightarrow x_1^2=7-3x_1\)
\(F=x_1^2-3x_2-2013=7-3x_1-3x_2-2013\\ F=-3\left(x_1+x_2\right)-2006\)
Mà theo Viét ta có \(x_1+x_2=-3\)
\(\Rightarrow F=\left(-3\right)\left(-3\right)-2006=-1997\)
\(x^2-3x^2+3x+2=-2x^2+2+3x=2\left(1-x^2\right)+3x=2\left(1+x\right)\left(1-x\right)+3x=2\cdot12\cdot\left(-10\right)+33=-240+33=-217\)
(có lẽ đây chưa phải là giải pháp tốt nhất)
\(x^3\)hay \(x^2\)hả bạn?