a) Thay \(x=1\) vào phương trình, ta được:

    \(1+2m+1+m^2-3m=0\) \(\Rightarrow m\in\varnothing\)

Vậy khi \(x=1\) thì phương trình vô nghiệm

b) Xét phương trình, ta có: \(\Delta=16m+1\)

Để phương trình có nghiệm \(\Leftrightarrow\Delta\ge0\) \(\Leftrightarrow m\ge-\dfrac{1}{16}\)

Vậy \(m\ge-\dfrac{1}{16}\)

a) thay m = 3 ta có pt:

x² + 10x + 3 = 0 

<=> xét delta phẩy 

25 - 3 = 22 

\(\left[{}\begin{matrix}x1=-5+\sqrt{22}\\x2=-5-\sqrt{22}\end{matrix}\right.\)

vậy S={ \(-5+\sqrt{22}\);\(-5-\sqrt{22}\)}

b) xét delta phẩy 

(m+2)² - m² + 6

= 4m +10 

để phương trình có 2 nghiệm x1;x2 thì delta phẩy ≥ 0 

=> m ≥ \(\dfrac{-10}{4}\)

theo Vi-ét ta có:

\(\left\{{}\begin{matrix}x1+x2=-2m-4\\x1x2=m^2-6\end{matrix}\right.\)

theo bài ra ta có:

x1² + x2² = 16

<=> (x1+x2)² - 2x1x2 = 16

=> 4m² + 16m + 16 - 2m² + 12 = 16

<=> 2m² + 16m + 12 = 0 

<=> m² + 8m + 6 = 0 

giải ra \(\left[{}\begin{matrix}m=-4+\sqrt{10}\\m=-4-\sqrt{10}\end{matrix}\right.\)

vậy m = \(-4+\sqrt{10}\) để pt có 2 nghiệm thỏa mãn hệ thức x1² + x2² = 16

( m = -4-\(\sqrt{10}\) loại)

cái này là lớp mấy thế bạn

7 nhé

=>x^2+x-1=0

Δ=1^2-4*1*(-1)=1+4=5>0

=>Phương trình luôn có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{-1-\sqrt{5}}{2}\\x_2=\dfrac{-1+\sqrt{5}}{2}\end{matrix}\right.\)

là sao ôg

\(x^2-2x+8< 0\)

\(\Leftrightarrow x^2-2x+1+7< 0\)

\(\Leftrightarrow\left(x-1\right)^2+7< 0\)

PTVN.

`x^2 - 2x + 8 < 0`

`<=> (x-1)^2 + 7 < 0`

`<=> (x-1)^2 < -7`

Vì `(x-1)^2 > -7` với mọi `x`

`=>` vô nghiệm 

Vậy `x \in RR`

\(\left(x^2+2>0\right)\left(2x-3\right)=0\Leftrightarrow x=\dfrac{3}{2}\)

Thay x=7+căn 2022 vào pt, ta được:

\(49+14\sqrt{2022}+2022-7-\sqrt{2022}+3m-2=0\)

=>\(3m+2062+13\sqrt{2022}=0\)

=.\(m=\dfrac{-2062-13\sqrt{2022}}{3}\)

a: Thay m=3 vào pt, ta được:

\(x^2-2\cdot\left(3-1\right)x+3^2-2\cdot3=0\)

\(\Leftrightarrow x^2-4x+3=0\)

=>(x-1)(x-3)=0

=>x=1 hoặc x=3

b: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-2m\right)\)

\(=\left(2m-2\right)^2-4\left(m^2-2m\right)\)

\(=4m^2-8m+4-4m^2+8m=4>0\)

Do đó: Phương trình luôn có hai nghiệm phân biệt

Thay x=-2 vào pt, ta được:

\(\left(-2\right)^2-2\cdot\left(-2\right)\cdot\left(m-1\right)+m^2-2m=0\)

\(\Leftrightarrow m^2-2m+4+4\left(m-1\right)=0\)

\(\Leftrightarrow m^2-2m+4+4m-4=0\)

=>m(m+2)=0

=>m=0 hoặc m=-2

Theo hệ thức Vi-et, ta được:

\(x_1+x_2=2\left(m-1\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x_2-2=2\cdot\left(-1\right)=-2\\x_2-2=2\cdot\left(-3\right)=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=0\\x_2=-4\end{matrix}\right.\)

c: \(x_1^2+x_2^2=4\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)

\(\Leftrightarrow\left(2m-2\right)^2-2\left(m^2-2m\right)=4\)

\(\Leftrightarrow4m^2-8m+4-2m^2+4m-4=0\)

\(\Leftrightarrow2m^2-4m=0\)

=>2m(m-2)=0

=>m=0 hoặc m=2

em cảm ơn ạ

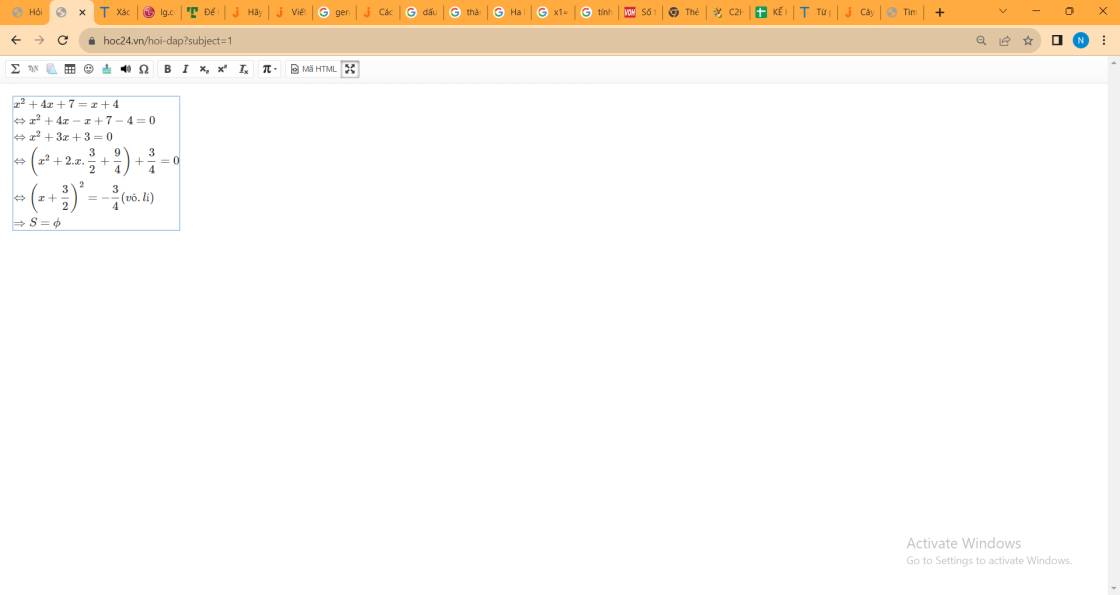
\(x^2+4x+7=x+4\\ \Leftrightarrow x^2+4x-x+7-4=0\\ \Leftrightarrow x^2+3x+3=0\\ \Leftrightarrow\left(x^2+2.x.\dfrac{3}{2}+\dfrac{9}{4}\right)+\dfrac{3}{4}=0\\ \Leftrightarrow\left(x+\dfrac{3}{2}\right)^2=-\dfrac{3}{4}\left(vô.lí\right)\\ \Rightarrow S=\phi\)

Bị lỗi hiển thị em hi

Em xem ha