2xy + 4y = x + 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn cần ghi đầy đủ điều kiện của x,y đề mọi người hỗ trợ tốt hơn.

M = 5 - x2 + 2x - 4y2 - 4y
= (- x2 + 2x - 1) + (- 4y2 - 4y - 1) + 7
= 7 - (x - 1)2 - (2y + 1)2\(\le7\)
Dấu "=" xảy ra khi x = 1 và y = - 0,5
(^~^)
M = - x2 + 2xy - 4y2 + 2x + 10y - 8
- M = x2 - 2xy + 4y2 - 2x - 10y + 8
= (y2 + 1 + x2 + 2y - 2xy - 2x) + (3y^2 - 12y + 12) - 5
\(=\left(y+1-x\right)^2+3\left(y-2\right)^2-5\ge-5\)
\(\Rightarrow M\le5\)
Dấu "=" xảy ra khi y = 2 và x = 3.

a) \(M=10x^2+6y+4y^2+4xy+2\)
\(=\left(10x^2+4xy+\dfrac{2}{5}y^2\right)+\left(\dfrac{18}{5}y^2+6y+\dfrac{5}{2}\right)-\dfrac{1}{2}\)
\(=10\left(x^2+\dfrac{2}{5}xy+\dfrac{1}{25}y^2\right)+\dfrac{18}{5}\left(y^2+\dfrac{5}{3}y+\dfrac{25}{36}\right)-\dfrac{1}{2}\)
\(=10\left(x+\dfrac{1}{5}y\right)^2+\dfrac{18}{5}\left(y+\dfrac{5}{6}\right)^2-\dfrac{1}{2}\ge-\dfrac{1}{2}\)
Đẳng thức xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{5}y=0\\y+\dfrac{5}{6}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\y=-\dfrac{5}{6}\end{matrix}\right.\)
b) \(H=-x^2+2xy-4y^2+2x+10y-8\)
\(=-x^2+2x\left(y+1\right)-\left(y^2+2y+1\right)-\left(3y^2-12y+7\right)\)
\(=-x^2+2x\left(y+1\right)-\left(y+1\right)^2-3\left(y^2-4y+4\right)+5\)
\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+5\le5\)
Đẳng thức xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x-y-1=0\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)
c) \(K=2x^2+2xy-2x+2xy+y^2\)
bn xem lại cái đề nhé, sao lại có 2 lần 2xy

\(A=-x^2+2xy-4y^2+2x+10y-8\)
\(=-\left(x^2-2xy+4y^2-2x-10y+8\right)\)
\(=-\left[\left(x-y-1\right)^2+3\left(y-2\right)^2-5\right]\)
\(=5-\left(x-y-1\right)^2-3\left(y-2\right)^2\le5\)
Dấu"=" xảy ra <=> \(\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}}\) <=> \(\hept{\begin{cases}x=3\\y=2\end{cases}}\)
Vậy MAX \(A=5\)khi \(x=3;\)\(y=2\)



\(P=\) \(x^2-2xy+4y^2-2x-10+8\)
\(=x^2-2xy+4y^2-2x-2\)
\(=x^2-2x\left(y+1\right)+\left(y+1\right)^2-\left(y+1\right)^2+4y^2-2\)
\(=\left(x-y-1\right)^2-y^2-2y-1+4y^2-2\)
\(=\left(x-y-1\right)^2+3y^2-2y-3\)
\(=\left(x-y-1\right)^2+3\left(y^2-\frac{2}{3}y-1\right)\)
\(=\left(x-y-1\right)^2+3\left(y^2-2y\frac{1}{3}+\frac{1}{9}-\frac{10}{9}\right)\)
\(=\left(x-y-1\right)^2+3\left(y-\frac{1}{3}\right)^2-\frac{10}{3}\)
\(\Rightarrow P\ge\frac{-10}{3}\)
Dấu ''='' xảy ra \(\Leftrightarrow\hept{\begin{cases}x-y-1=0\\y-\frac{1}{3}=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x-y=1\\y=\frac{1}{3}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=1+\frac{1}{3}=\frac{4}{3}\\y=\frac{1}{3}\end{cases}}\)
Vậy giá trị nhỏ nhất của P là \(\frac{-10}{3}\Leftrightarrow\hept{\begin{cases}x=\frac{4}{3}\\y=\frac{1}{3}\end{cases}}\)

ta có:
M=x^2+4y^2-2x-2xy-10y+8
=(x^2-2xy+y^2)-(2x-2y)+3y^2-12y+8
=(x-y)^2-2(x-y)+1+3(y^2-4y+4)-(13-8)
=(x-y-1)^2+3(y-2)^2-5
vì (x-y-1)^2\(\ge0\)với mọi x,y
3(y-2)^2\(\ge0\)với mọi y
suy ra (x-y-1)^2+3(y-2)^2-5\(\ge-5\)với mọi x,y
dấu "=" xảy ra\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x-y-1=0\\y-2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x-y=1\\y=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)
Vậy GTNN của M là -5 khi \(\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)
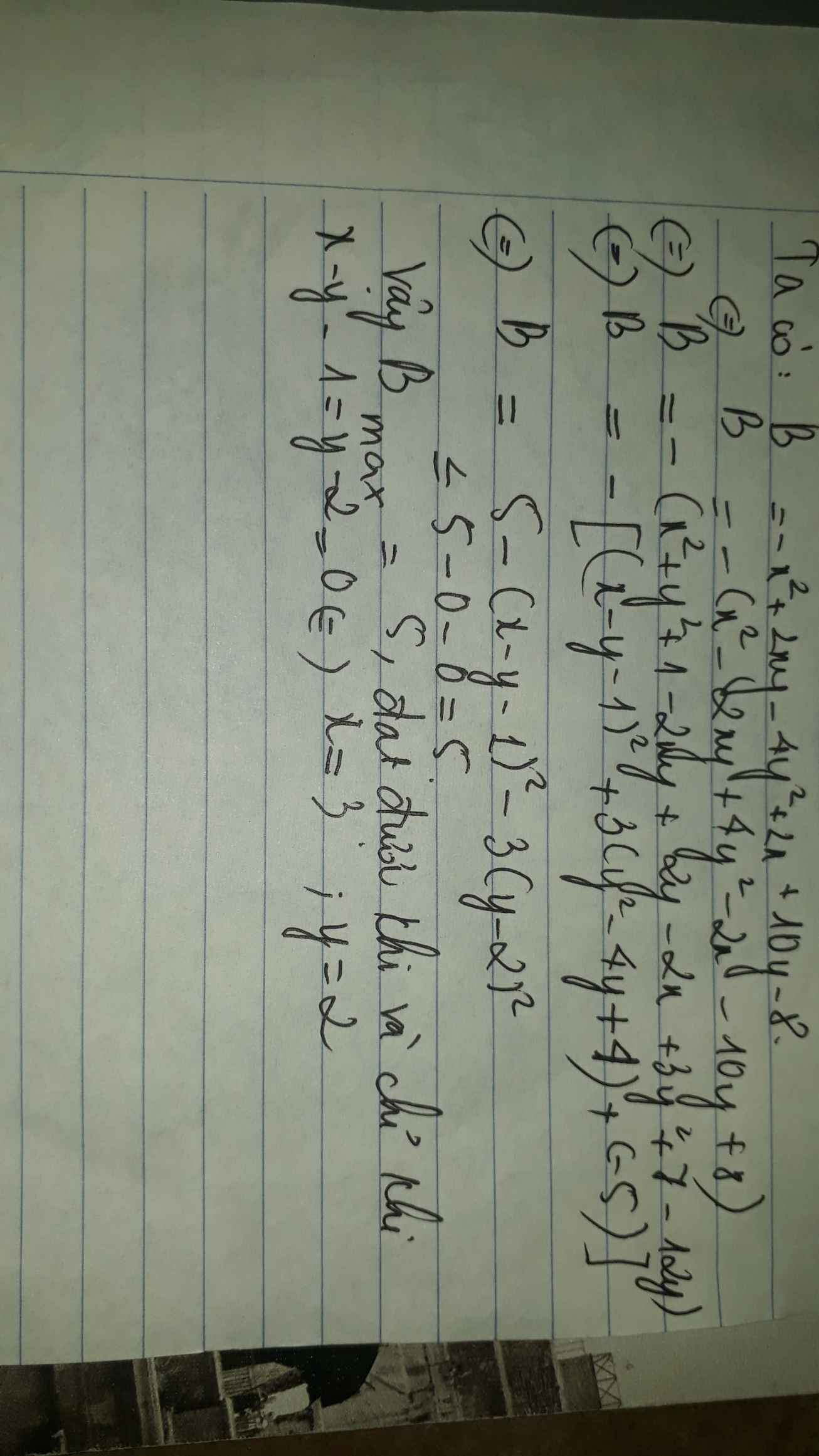
2xy+4y=x+8
2y(x+4)=(x+4)+4
2y(x+4)-(x+4)=4
(x+4)(2y-1)=4 .Sau đó tìm U(4)
Tiếp bạn từ kẻ bảng làm