cho tam giác ABC có AB< AC M là trung điểm của BC so sánh Góc BAM và góc MAC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trên tia \(AM\) của tam giác \(ABC\) lấy điểm \(I\) sao cho \(AM=IM\)
Ta có: \(AM=IM\) (theo giả thiết)
góc \(M_1\) \(=\) góc \(M_2\) (đối đỉnh)
\(MC=MB\) (do \(M\) là trung điểm của \(BC\))
nên \(\Delta AMC=\Delta IMB\) \(\left(cgc\right)\)
suy ra góc \(MAC\) \(=\) góc \(MIB\) (hai góc tương ứng)
Do đó, \(BI=AC>AB\)
Khi đó, xét \(\Delta ABI\) có \(BI>AB\)
nên góc \(BAI\) \(>\) góc \(BIA\)
\(\Leftrightarrow\) góc \(BAM\) \(>\) góc \(MAC\)



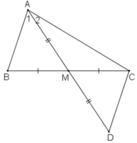
Trên tia đối tia MA lấy điểm D sao cho MD = MA
Xét ΔAMB và ΔDMC, ta có:
MA = MD (theo cách vẽ)
∠(AMB) = ∠(DMC) (đối đỉnh)
MB = MC (gt)
Suy ra: ΔAMB = ΔDMC (c.g.c)
Suy ra: AB = CD (2 cạnh tương ứng)
và ∠D = ∠A1(2 góc tương ứng) (1)
Mà AB < AC (gt)
nên: CD < AC
Trong ΔADC, ta có: CD < AC
Suy ra: ∠D > ∠A2(đối diện cạnh lớn hơn là góc lớn hơn) (2)
Từ (1) và (2) suy ra: ∠A1 > ∠A2hay ∠(BAM) > ∠(MAC) .



a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{4}=\dfrac{AC}{5}=\dfrac{BC}{6}=\dfrac{AB+AC+BC}{4+5+6}=\dfrac{30}{15}=2\)
Do đó: AB=8cm; AC=10cm; BC=12cm
=>\(\widehat{C}< \widehat{B}< \widehat{A}\)
b: \(\cos MAB=\dfrac{AB^2+AM^2-BM^2}{2\cdot AB\cdot AM}=\dfrac{AB^2+AM^2-CM^2}{2\cdot AB\cdot AM}\)
\(\cos MAC=\dfrac{AM^2+AC^2-MC^2}{2\cdot AM\cdot AC}\)
mà \(\dfrac{AB^2+AM^2-MC^2}{2\cdot AM\cdot AC}< \dfrac{AM^2+AC^2-MC^2}{2\cdot AM\cdot AC}\)
nên \(\widehat{MAB}>\widehat{MAC}\)
ấn đúng 0
đáp án và lời giải sẽ hiện ra trước mắt