\(\dfrac{2}{3}-\left|x-2,4\right|=\dfrac{1}{2}\)

\(\left|x-2,4\right|=\dfrac{2}{3}-\dfrac{1}{2}\)

\(\left|x-2,4\right|=\dfrac{1}{6}\)

*) Với \(x\ge2,4\) ta có:

\(x-2,4=\dfrac{1}{6}\)

\(x=\dfrac{1}{6}+2,4\)

\(x=\dfrac{77}{30}\) (nhận)

*) Với \(x< 2,4\) ta có:

\(x-2,4=-\dfrac{1}{6}\)

\(x=-\dfrac{1}{6}+2,4\)

\(x=\dfrac{67}{30}\) (nhận)

Vậy \(x=\dfrac{67}{30};x=\dfrac{77}{30}\)

a, \(\dfrac{3}{7}\)\(x\) - 0,4 = - \(\dfrac{17}{35}\)

    \(\dfrac{3}{7}\)\(x\)         = - \(\dfrac{17}{35}\) + 0,4

     \(\dfrac{3}{7}\)\(x\)       = - \(\dfrac{3}{35}\)

        \(x\)       = - \(\dfrac{3}{35}\): \(\dfrac{3}{7}\)

        \(x\)       = - \(\dfrac{1}{5}\)

b, 0,2.(\(x\) - 3) +2,4 = 10

    0,2.(\(x\) - 3)          = 10 - 2,4

    0,2.(\(x\) - 3)          = 7,6

           \(x\) - 3            = 7,6:0,2

           \(x\) - 3            = 38

            \(x\)                = 38 + 3

             \(x\)                = 41

\(a,5,2x+7\dfrac{2}{5}=6\dfrac{3}{4}\\ \Rightarrow\dfrac{26}{5}x+\dfrac{37}{5}=\dfrac{27}{4}\\ \Rightarrow\dfrac{26}{5}x=-\dfrac{13}{20}\\ \Rightarrow x=-\dfrac{1}{8}\\ b,2,4:\left(\dfrac{-1}{2}-x\right)=1\dfrac{3}{5}\\ \Rightarrow\dfrac{12}{5}:\left(\dfrac{-1}{2}-x\right)=\dfrac{8}{5}\\ \Rightarrow\dfrac{-1}{2}-x=\dfrac{3}{2}\\ \Rightarrow x=-2\)

a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)

Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)

=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)

=>\(4⋮\sqrt{x}-3\)

=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)

=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)

=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)

=>\(x\in\left\{16;4;25;1;49\right\}\)

b: 

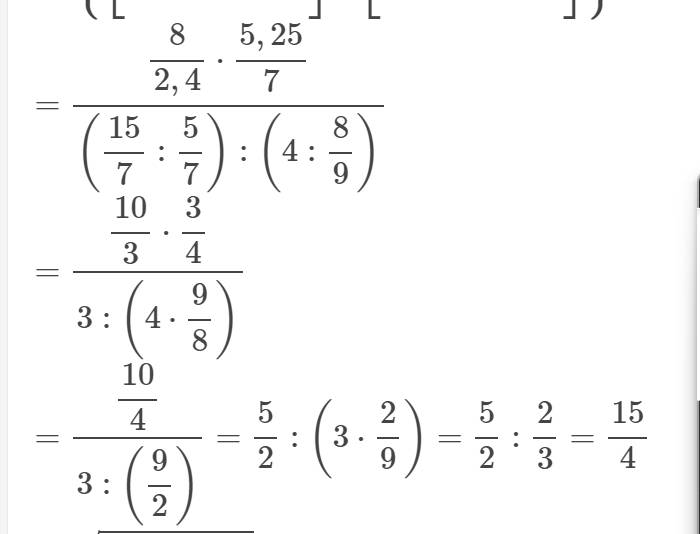
Bài 1: Ta có: \(4\dfrac{3}{5}+\dfrac{7}{10}< X< \dfrac{20}{3}\)

\(\dfrac{23}{5}+\dfrac{7}{10}< X< \dfrac{20}{3}\)

\(\dfrac{138}{30}< X< \dfrac{200}{3}\)

\(\Rightarrow X\in\left\{\dfrac{160}{30};\dfrac{161}{30};\dfrac{162}{30};...;\dfrac{198}{30};\dfrac{199}{30}\right\}\)

Bài 2: \(X-2019\dfrac{2}{13}=3\dfrac{7}{26}+4\dfrac{7}{52}\)

\(\Rightarrow X-\dfrac{26249}{13}=\dfrac{85}{26}+\dfrac{215}{52}\)

\(\Rightarrow X-\dfrac{26249}{13}=\dfrac{385}{52}\)

\(\Rightarrow X=\dfrac{105381}{52}\)

Các đa thức là: \( - {x^2} + 3x + 1;\dfrac{x}{{\sqrt 5 }};2024;3{x^2}{y^2} - 5{x^3}y + 2,4.\)

\(1.x-\dfrac{2}{3}\times\left(x+9\right)=1\)

\(x-\dfrac{2}{3}\times x-6=1\)

\(x\times\left(1-\dfrac{2}{3}\right)=7\)

\(x\times\dfrac{1}{3}=7\)

\(x=21\)

\(2.x-\dfrac{11}{15}=\dfrac{3+x}{5}\)

\(\dfrac{15x}{15}-\dfrac{11}{15}=\dfrac{9+3x}{15}\)

\(15x-11=9+3x\)

\(12x=20\)

\(x=\dfrac{5}{3}\)

a) \(\left|x-1\right|=5\)

\(\Rightarrow\orbr{\begin{cases}x-1=5\\x-1=-5\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=6\\x=-4\end{cases}}\)

b) \(\left|x-0,5\right|=2,4\)

\(\Rightarrow\orbr{\begin{cases}x-0,5=2,4\\x-0,5=-2,4\end{cases}}\Rightarrow\orbr{\begin{cases}x=2,9\\x=-1,9\end{cases}}\)

c) \(2\left|3x-1\right|-1=6\)

\(\Leftrightarrow2\left|3x-1\right|=7\)

\(\Leftrightarrow\left|3x-1\right|=3,5\)

\(\Rightarrow\orbr{\begin{cases}3x-1=3,5\\3x-1=-3,5\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}3x=4,5\\2x=-2,5\end{cases}\Rightarrow\orbr{\begin{cases}x=1,5\\-1,25\end{cases}}}\)

a)4 hoặc -4

b)1,9 hoặc -1,9

c)1,5

a: ĐKXĐ: x<>0; x<>1

\(P=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\)

\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\dfrac{x\left(x-1\right)}{x+1}=\dfrac{x^2}{x-1}\)

b: |2x+1|=3

=>x=1(loại); x=-2(nhận)

Khi x=-2 thì P=4/-3=-4/3

c: P=-1/2

=>x^2/x-1=-1/2

=>2x^2=-x+1

=>2x^2+x-1=0

=>2x^2+2x-x-1=0

=>(x+1)(2x-1)=0

=>x=1/2; x=-1