-Ta cần phải lấy bóng ở trong hộp ghi Trắng-Đen, bởi vì họ dán nhãn sai nên trong đó có 2 quả bóng cùng màu trắng hoặc đen.

-Khi ta lấy được quả bóng có 1 màu nào đó thì ta sẽ biết được hộp Trắng-Đen chứa 2 quả bóng cùng màu ấy. Gọi màu đó là màu a và màu còn lại là màu b thì:

-Khi xác định màu bóng trong  hộp dán nhãn a-a thì chắc chắn trong đó sẽ không có 2 màu bóng a-b được bởi nếu vậy thì màu hộp a-b đã chứa bóng màu a-a hộp a-a sẽ chứa bóng màu a-b => hộp b-b sẽ chứa bóng màu b-b, lại trái đề bài là họ đều dán nhãn sai. Vậy trong hộp a-a sẽ có màu bóng là b-b và hộp b-b sẽ chứa bóng màu a-b.

Ta đã xác định được màu bóng trong 3 hộp!

bạn Ngô Văn Phương trả lời rối quá

a) \(P\left( A \right) = \frac{6}{{10}} = \frac{3}{5};P\left( B \right) = \frac{7}{8}\)

Không gian mẫu là tập hợp số cách Bạn Long lấy được một quả bóng từ hộp I và Bạn Hải lấy một quả bóng từ hộp II do đó \(n\left( \Omega  \right) = 10.8 = 80\)

C: “Bạn Long lấy được quả màu trắng và bạn Hải lấy được quả màu đen”

Công đoạn 1: Bạn Long lấy được quả màu trắng có 6 cách

Công đoạn 2. Bạn Hải lấy được quả màu đen có 7 cách

Theo quy tắc nhân, tập hợp C có 6.7 = 42 (phần tử)

\(P\left( C \right) = P\left( {AB} \right) = \frac{{n\left( C \right)}}{{n\left( \Omega  \right)}} = \frac{{42}}{{80}} = \frac{{21}}{{40}}\)

b) \(P\left( A \right).P\left( B \right) = \frac{3}{5}.\frac{7}{8} = \frac{{21}}{{40}}\)

Vậy P(AB) = P(A).P(B).

Lấy bóng ở hộp TT. Nếu đó là bóng đỏ thì hộp đó là bóng đỏ( vì nhãn dán nhầm) thì hộp XT là bóng xanh, đỏ và hộp XX là bóng xanh. Nếu đó là bóng xanh thì hộp đó là bóng xanh, hộp XX là bóng đỏ, xanh và hộp XT là bóng đỏ

Nguyễn Nam Cao trả lời sai mà cũng được 1**** nhỉ =)) Vì bạn đã làm mất thời gian của tôi lên giờ tôi cũng chả thiết nữa

Ở ngay vế đầu của lời giải của bạn có 1 sai lầm:

- Nó ghi sai nhãn lên ở hộp Trắng Trắng sẽ có 2 trường hợp:

=> TH1: Là hộp Xanh Trắng

=> TH2: Là hộp Xanh Xanh

Theo như câu trả lời của bạn thì " Nếu đó là 'bóng đỏ?' thì hộp đó là bóng đỏ" 

Tôi thay từ đỏ là từ xanh ở câu tl của bạn cho dễ hiểu nhé! " Nếu đó là bóng xanh thì hộp đó là hộp Xanh Xanh " Ý bạn là vậy?

Sao không phải là hộp Xanh Trắng? Sai ngay ở cơ hội đầu tiên => Sai cả bài

Không gian mẫu: \(C_{20}^5\)

a. Số biến cố thuận lợi: \(C_{12}^3.C_8^2\)

Xác suất: \(P=\dfrac{C_{12}^3.C_8^2}{C_{20}^5}=...\)

b. Các trường hợp thỏa mãn: (0 trắng, 5 đen), (1 trắng, 4 đen), (2 trắng, 3 đen)

\(\Rightarrow C_8^5+C_{12}^1.C_8^4+C_{12}^2.C_8^3\)

Xác suất: \(P=\dfrac{C_8^5+C_{12}^1.C_8^4+C_{12}^2.C_8^3}{C_{20}^5}=...\)

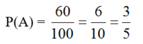
a) Không gian mẫu là kết quả của việc lấy ngẫu nhiên 1 quả cầu ở hộp thứ nhất và một quả cầu ở hộp thứ hai

+ Có 10 cách lấy 1 quả cầu bất kì ở hộp 1 và có 10 cách lấy 1 quả cầu bất kì ở hộp 2. Nên số phần tử của không gian mẫu là;

⇒ n(Ω) = 10.10 = 100.

A: “ Quả cầu lấy từ hộp thứ nhất trắng”

⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 10 cách lấy quả cầu ở hộp B

⇒ n(A) = 6.10 = 60.

B: “Quả cầu lấy từ hộp thứ hai trắng”

⇒ Có 4 cách lấy quả cầu màu trắng ở hộp B và 10 cách lấy quả cầu ở hộp A

⇒ n(B) = 4.10 = 40.

A.B: “Cả hai quả cầu lấy ra đều trắng”

⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 4 cách lấy quả cầu màu trắng ở hộp B

⇒ n(A.B) = 6.4 = 24.

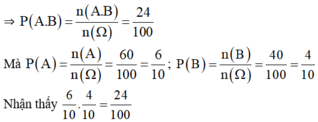
hay P(A.B) = P(A).P(B)

⇒ A và B là biến cố độc lập.

b) Gọi C: “Hai quả cầu lấy ra cùng màu”.

Ta có: A− : “Quả cầu lấy ra từ hộp thứ nhất màu đen”

B− : “ Quả cầu lấy ra từ hộp thứ hai màu đen”

⇒A−.B− : “Cả hai quả cầu lấy ra đều màu đen”

Nhận thấy A.B và A−.B− xung khắc (Vì không thể cùng lúc xảy ra hai trường hợp 2 quả cầu lấy ra cùng trắng và cùng đen)

Và C=(A.B)∪(A−.B−)

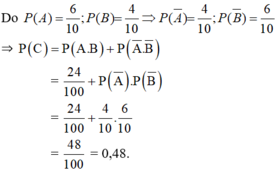
c) C− : “Hai quả cầu lấy ra khác màu”

⇒ P(C− )=1-P(C)=1-0,48=0,52

Không gian mẫu: \(C_{10}^3\)

a. Xác suất: \(\dfrac{C_4^2.C_6^1}{C_{10}^3}=...\)

b. \(P=\dfrac{C_4^2C_6^1+C_4^3}{C_{10}^3}=...\)

c. \(P=\dfrac{C_6^3}{C_{10}^3}=...\)