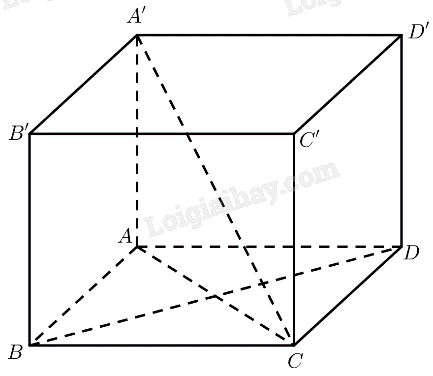
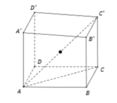
Cho hình hộp A'B'C'D'.ABCD, xác định tiết diện của hình hộp tạo bởi mặt phẳng P đi qua điểm M bất kì nằm trên cạnh BC và mặt phẳng P song song với mặt phẳng ACD'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a sai, b đúng, c sai, d đúng
Hình hộp là hình lăng trụ tứ giác có đáy là hình bình hành

Đáp án B
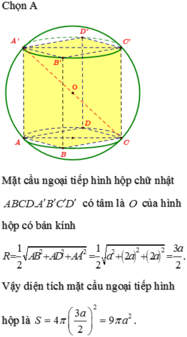
Ta có: A C = A B 2 + B C 2 = a 5
Bán kính mặt cầu ngoại tiếp là 3 a 2 ⇒ A C ' = 3 a
Xét tam giác A C C ' vuông tại C, ta có: C C ' = A C ' 2 - A C 2 = 2 a
Thể tích hình hộp là:
V = C C ' . S A B C D = 2 a . a . 2 a = 4 a 3

Bài 1:
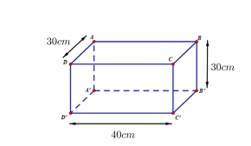
a/ Hình hộp chữ nhật ABCD. A'B'C'D'.
b/ Hai mặt đáy: ABCD và A'B'C'D'.
c/ Các mặt bên: AA'D'D; DCC'D'; CBB'C'; ABB'A'.
d/ Các cạnh bên: AA'; BB'; CC'; DD'.
e/ Đường chéo: AC'; BD'; DB'; CA'.
g/ Diện tích xung quanh của hình lăng trụ đứng đó là:
\(2.\left(40+30\right).30=4200\) ( cm2 )
h/ Diện tích một mặt đáy của hình lăng trụ đứng là:
\(40.30=1200\) ( cm2 )
Diện tích toàn phần của hình lăng trụ đứng đó là:
\(4200+1200.2=6600\) ( cm2 )
Thể tích của hình lăng trụ đứng đó là:
\(40.30.30=36000\) ( cm3 )
\(#WendyDang\)
a) Tên hình hộp chữ nhật:
ABCD.A'B'C'D'
b) Hai mặt đáy của hình hộp chữ nhật:
ABCD và A'B'C'D'
c) Các mặt bên của hình hộp chữ nhật:
ABB'A', BCC'B', CDD'C', ADD'A'
d) Các cạnh bên của hình hộp chữ nhật:
AA', BB', CC', DD'
e) Các đường chéo của hình hộp chữ nhật:
AC', BD', CA', DB'
g) Diện tích xung quanh của hình hộp chữ nhật:
(30 + 40) . 2 . 30 = 4200 (cm²)
h) Diện tích toàn phần:
4200 + 2.30.40 = 6600 (cm²)
Thể tích:
30.40.30 = 36000 (cm³)

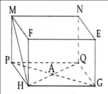
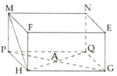
a) Tên 5 đỉnh: M, N, F, E, P
Tên 4 mặt: MNEF, MNQP, PQGH, NEGQ.
Lưu ý: HS có thể liệt kê tên các đỉnh, các mặt khác.
b) Tên các cạnh: MN, NE, EF, FM, PQ, QG, GH, HP, MP, FH, NQ, EG

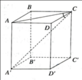
a) Xét tam giác \(AB{\rm{D}}\) có: \(AB = A{\rm{D}} = B{\rm{D}} = a\)
\( \Rightarrow \Delta AB{\rm{D}}\) đều \( \Rightarrow \widehat {BA{\rm{D}}} = {60^ \circ } \Rightarrow \widehat {ABC} = {180^ \circ } - \widehat {BA{\rm{D}}} = {120^ \circ }\)
Xét tam giác \(AB{\rm{C}}\) có:
\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC} = a\sqrt 3 \)
\(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta AA'C\) vuông tại \(A\)
\( \Rightarrow AA' = \sqrt {A'{C^2} - A{C^2}} = a\)
b) Ta có:
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = {S_{A'B'C'D'}} = AB.AC.\sin \widehat {BAC} = \frac{{{a^2}\sqrt 3 }}{2}\\{S_{ABB'A'}} = {S_{C{\rm{DD}}'{\rm{C}}'}} = AB.AA' = {a^2}\\{S_{A{\rm{DD}}'A'}} = {S_{BCC'B'}} = A{\rm{D}}.AA' = {a^2}\end{array}\)
Tổng diện tích các mặt của hình hộp là:
\(S = {S_{ABC{\rm{D}}}} + {S_{A'B'C'D'}} + {S_{ABB'A'}} + {S_{C{\rm{DD}}'{\rm{C}}'}} + {S_{A{\rm{DD}}'A'}} + {S_{BCC'B'}} = 2.\frac{{{a^2}\sqrt 3 }}{2} + 4.{a^2} = \left( {4 + \sqrt 3 } \right){a^2}\)

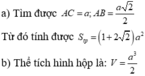
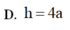
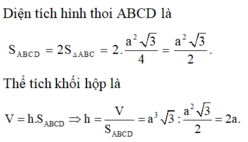
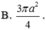
@mọi người giúp mình với