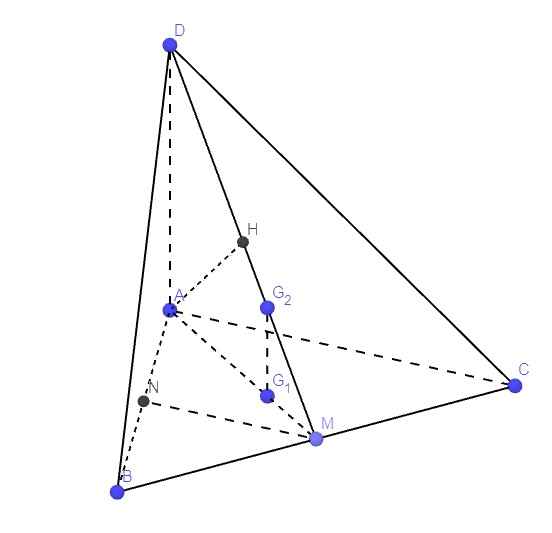
Cho tứ diện ABCD đáy ΔABC cân, DA \(\perp\) đáy, AB=AC=a, BC = \(\dfrac{6}{5}\)a. M là trung điểm BC. Vẽ AH \(\perp\)MD. (H thuặc đường thẳng MD)
a) C/M AH \(\perp\) (BCD)
b, Cho AD = \(\dfrac{4}{3}\)a. Tính (\(\widehat{AC,DM}\))
c, Gọi G1, G2 lần lượt là các trọng tâm của tam giác ABC và tam giác DBC. CM: G1G2 \(\perp\)(ABC)

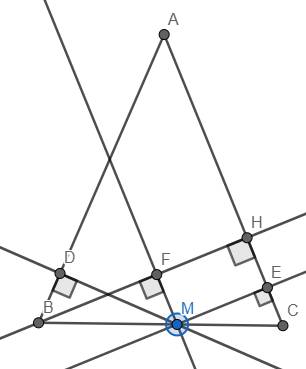

a: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
mà DA vuông góc (ABC)
nên BC vuông góc (DAM)
=>CB vuông góc AH
mà DM vuông góc AH
nên AH vuông góc (DBC)
b: Kẻ MN//AC(N thuộc AB)
=>(DM;AC)=(DM;MN)=góc DMN hoặc =180 độ-góc DMN
MN=1/2AC=a/2; AN=a/2
DN^2=DA^2+AN^2=89/100a^2
=>AM^2=AB^2-MA^2=a^2-9/25a^2=16/25a^2
=>AM=4/5a
AD=4/5a
=>\(DM=\dfrac{4a\sqrt{2}}{5}\)
DN^2=DM^2+MN^2-2*DM*MN*cosDMN
=>\(\cos DMN=\dfrac{2\sqrt{2}}{5}\)
=>\(\left(AC;DM\right)\simeq56^0\)
c: G1G2//DA
mà DA vuông góc (ABC)
nên G1G2 vuông góc (ABC)