Giúp em câu 18 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


17)
a)
\(CH_3-CH_3\underrightarrow{t^o,xt}CH_2=CH_2+H_2\)
\(CH_2=CH_2+Br_2\rightarrow CH_2Br-CH_2Br\)
\(CH_2Br-CH_2Br+2KOH\underrightarrow{ancol,t^o}CH\equiv CH+2KBr+2H_2O\)
\(CH\equiv CH+H_2O\underrightarrow{HgSO_4,H_2SO_4}CH_3CHO\)
b)
\(CaC_2+2H_2O\rightarrow Ca\left(OH\right)_2+CH\equiv CH\)
\(2CH\equiv CH\underrightarrow{đime.hóa}CH\equiv C-CH=CH_2\)
\(CH\equiv C-CH=CH_2+H_2\underrightarrow{t^o,Pd/PbCO_3}CH_2=CH-CH=CH_2\)
\(nCH_2=CH-CH=CH_2\underrightarrow{t^o,p,Na}\left(-CH_2-CH=CH-CH_2-\right)_n\)
c)
\(Al_4C_3+12H_2O\rightarrow4Al\left(OH\right)_3+3CH_4\)
\(2CH_4\underrightarrow{1500^oC,làm.lạnh.nhanh}CH\equiv CH+3H_2\)
\(CH\equiv CH+H_2\underrightarrow{t^o,Pd/PbCO_3}CH_2=CH_2\)
\(CH_2=CH_2+H_2O\underrightarrow{t^o,H_2SO_4}CH_3-CH_2OH\)
\(CH_3-CH_2OH+3O_2\underrightarrow{t^o}2CO_2+3H_2O\)
d)
\(CH_3-CH_2OH\underrightarrow{170^oC,H_2SO_4}CH_2=CH_2+H_2O\)
\(CH_2=CH_2+HCl\rightarrow CH_3-CH_2Cl\)
\(CH_3-CH_2Cl+KOH\underrightarrow{t^o,ancol}CH_2=CH_2+KCl+H_2O\)
\(nCH_2=CH_2\underrightarrow{t^o,p,xt}\left(-CH_2-CH_2-\right)_n\)
\(\)
18)
- Trích một ít các chất làm mẫu thử
a)
- Cho các khí tác dụng với dd AgNO3/NH3
+ Không hiện tượng: C2H6, C2H4 (1)
+ Kết tủa vàng: C2H2
\(C_2H_2+2AgNO_3+2NH_3\rightarrow C_2Ag_2+2NH_4NO_3\)
- Dẫn các khí còn lại ở (1) tác dụng với dd Br2 dư:
+ dd nhạt màu dần: C2H4
\(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
+ Không hiện tượng: C4H10
b)
- Dẫn các khí qua dd AgNO3/NH3:
+ Không hiện tượng: C4H10, \(CH_3-C\equiv C-CH_3\) (1)
+ Kết tủa vàng: \(CH\equiv C-CH_2-CH_3\)
\(CH\equiv C-CH_2-CH_3+AgNO_3+NH_3\rightarrow CAg\equiv C-CH_2-CH_3\downarrow+NH_4NO_3\)
- Dẫn các khí còn lại ở (1) tác dụng với dd Br2 dư
+ dd nhạt màu dần: \(CH_3-C\equiv C-CH_3\)
\(CH_3-C\equiv C-CH_3+2Br_2\rightarrow CH_3-CBr_2-CBr_2-CH_3\)
+ Không hiện tượng: C2H6
c)
- Dẫn các khí qua dd AgNO3/NH3:
+ Kết tủa vàng: \(CH\equiv C-CH_3\)
\(CH\equiv C-CH_3+AgNO_3+NH_3\rightarrow CAg\equiv C-CH_3\downarrow+NH_4NO_3\)
+ Không hiện tượng: C2H6, \(CH_2=CH-CH=CH_2\) (1)
- Dẫn các khí còn lại ở (1) tác dụng với dd Br2 dư
+ dd nhạt màu dần: \(CH_2=CH-CH=CH_2\)
\(CH_2=CH-CH=CH_2+2Br_2\rightarrow CH_2Br-CHBr-CHBr-CH_2Br\)
+ Không hiện tượng: C2H6


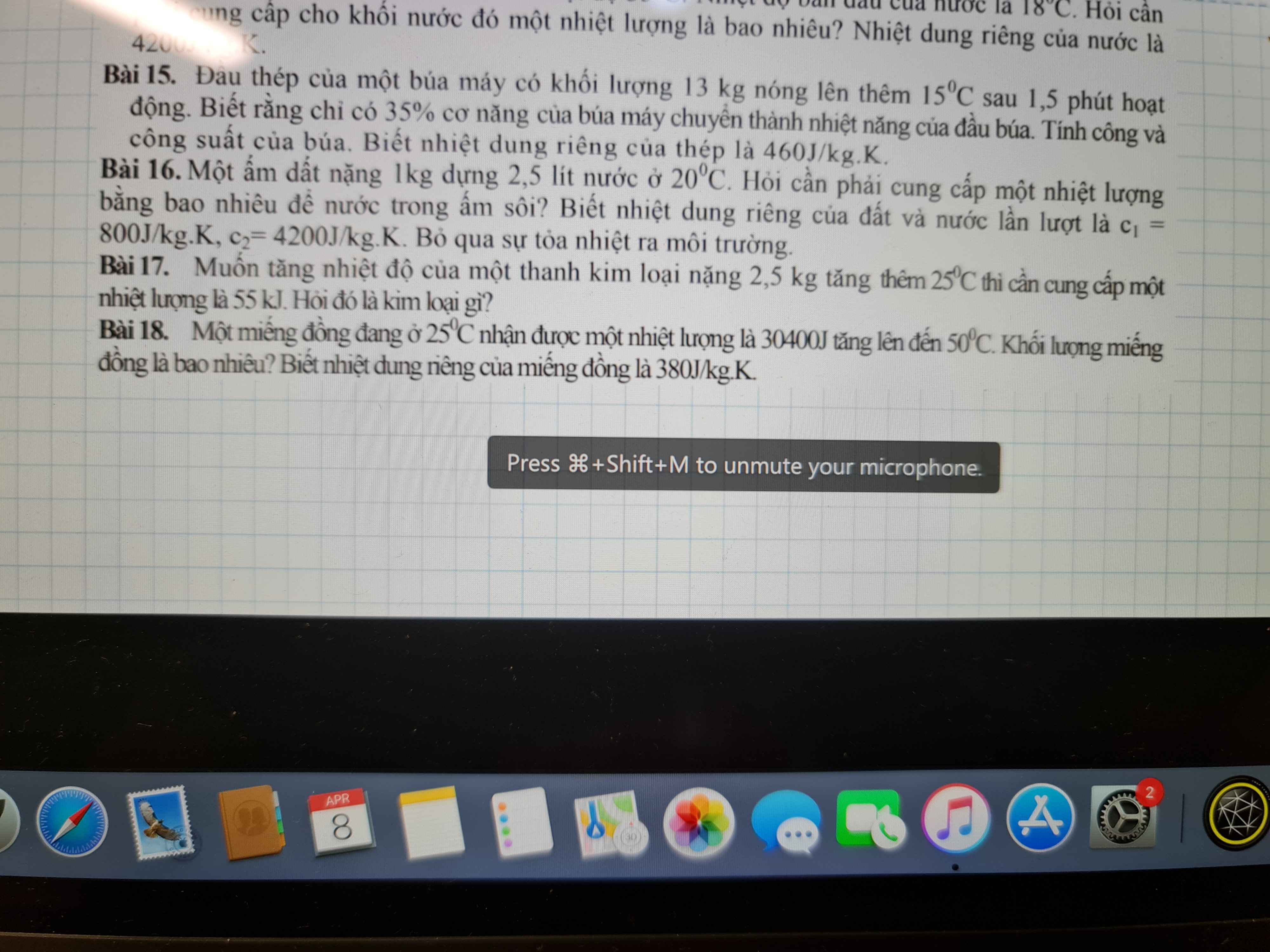
Câu 18.
Nhiệt lượng miếng đồng thu vào:
\(Q=mc\left(t_2-t_1\right)\)
\(\Rightarrow30400=m\cdot380\cdot\left(50-20\right)\)
\(\Rightarrow m=2,67kg\)


\(A=\left\{1;2;5;10;17\right\}\)
\(\left(x^2-4\right)\left(2x^2-x-1\right)=0\Rightarrow\left[{}\begin{matrix}x^2-4=0\\2x^2-x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm2\\x=1\\x=-\dfrac{1}{2}\notin Z\end{matrix}\right.\) \(\Rightarrow B=\left\{-2;1;2\right\}\)
\(\Rightarrow A\backslash B=\left\{5;10;17\right\}\)

152+ (−73)− (−18)− 127.
= 152 − 73 + 18 − 127.
= (152 + 18) - (73 + 127).
= 170 - 200 = -30.
= [152 - (-18)] - [127 - (-73)]
= (152 + 18) – (127 + 73)
= 170 - 200
= - 30

\(2sin3x+1=0\Leftrightarrow sin3x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=-\dfrac{\pi}{6}+k2\pi\\3x=\dfrac{7\pi}{6}+n2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{18}+\dfrac{k2\pi}{3}\\x=\dfrac{7\pi}{18}+\dfrac{n2\pi}{3}\end{matrix}\right.\)
\(x\in\left(-\dfrac{25\pi}{18};\dfrac{31\pi}{18}\right)\Rightarrow\left\{{}\begin{matrix}-\dfrac{25\pi}{18}< -\dfrac{\pi}{18}+\dfrac{k2\pi}{3}\le< \dfrac{31\pi}{18}\\-\dfrac{25\pi}{18}< \dfrac{7\pi}{18}+\dfrac{n2\pi}{3}< \dfrac{31\pi}{18}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-2< k< \dfrac{8}{3}\\-\dfrac{8}{3}< n< 2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=\left\{-1;0;1;2\right\}\\n=\left\{-2;-1;0;1\right\}\end{matrix}\right.\)
\(\Rightarrow\) Pt có 8 nghiệm trên khoảng đã cho

Bài 17:
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{BH}{CH}=\dfrac{c^2}{b^2}\)

\(\lim\dfrac{3.2^{n+1}-2.3^n}{4+3^n}=\lim\dfrac{6.\left(\dfrac{2}{3}\right)^n-2}{4.\left(\dfrac{1}{3}\right)^n+1}=\dfrac{0-2}{0+1}=-2\)

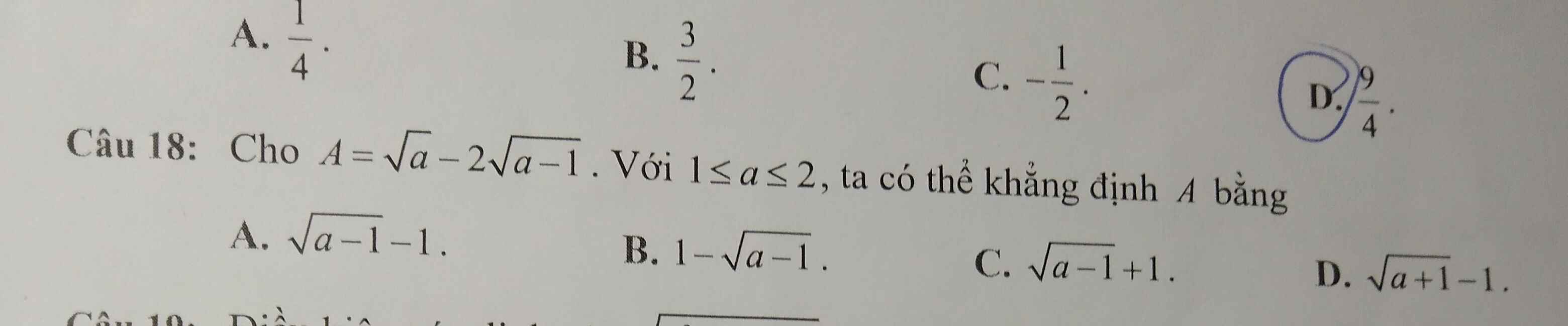




a.
\(\Delta=\left(2k-1\right)^2-4\left(2k-2\right)=4k^2-12k+9=\left(2k-3\right)^2\ge0;\forall k\)
\(\Rightarrow\) Phương trình luôn có nghiệm với mọi k
b.
Theo hệ thức Viet: \(x_1+x_2=2k-1\)